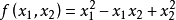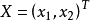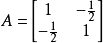半正定埃爾米特二次型

正定埃爾米特二次型是與實數域上正定二次型相對應的概念。正定、半正定、負定、半負定的埃爾米特二次型統稱為定型的；不定的埃爾米特二次型稱為不定型的。

基本介紹

• 中文名：半正定埃爾米特二次型 
• 外文名：positive semi-definite Hermitian quadratic form
• 適用範圍：數理科學

簡介

正定埃爾米特二次型是與實數域上正定二次型相對應的概念。

對於變數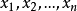 的任何複數值，埃爾米特二次型 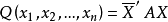的值都是實數。設 a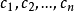是任意不全為零的複數。

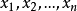
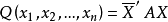
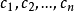
1、若恆有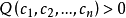，則 Q 稱為正定二次型。

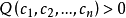
2、若恆有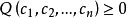，則 Q 稱為半正定二次型。

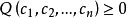
3、若恆有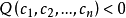，則 Q 稱為負定二次型。

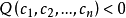
4、若恆有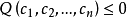，則 Q 稱為半負定二次型。

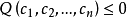
5、其他情形的 Q 稱為不定二次型。

正定、半正定、負定、半負定的埃爾米特二次型統稱為定型的；不定的埃爾米特二次型稱為不定型的。

埃爾二次型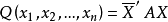是正定的充分必要條件為：Q 的矩陣 A 的各階順序主子式都大於零。

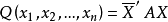
正定二次型

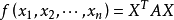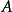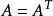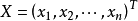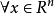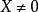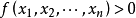設，其中矩陣是對稱陣，即，為列向量，若，，有，則稱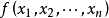為正定二次型，稱實對稱矩陣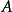正定。

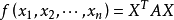
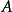
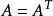
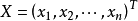
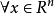
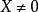
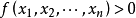
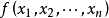
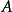
例如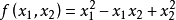，即為正定二次型，其中，。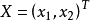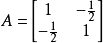