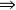若對任何非零向量x,實二次型f(x)如果對任何x≠0都有f(x)>0,則稱f為正定二次型,並稱矩陣A是正定的,記之A>0。
基本介紹
- 中文名:正定二次型
- 外文名:positive definite quadratic form
定義,性質,判定方法,行列式法,正慣性指數法,
定義
設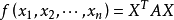 ,其中矩陣
,其中矩陣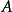 是對稱陣,即
是對稱陣,即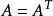 ,
,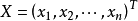 為列向量,若
為列向量,若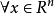 ,
,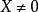 ,有
,有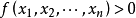 ,則稱
,則稱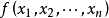 為正定二次型,稱實對稱矩陣
為正定二次型,稱實對稱矩陣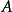 正定。
正定。
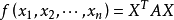
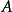
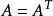
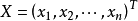
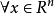
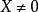
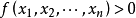
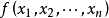
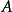
例如,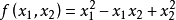 即為正定二次型,其中
即為正定二次型,其中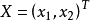 ,
,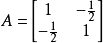 。
。
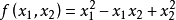
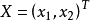
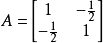
性質
(1) 階實對稱矩陣
階實對稱矩陣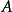 正定
正定

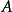
(2)若 階實對稱矩陣
階實對稱矩陣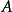 和
和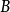 正定,
正定,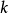 為實數,則
為實數,則

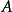
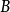
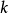
①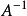 (逆)、
(逆)、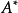 (伴隨矩陣)、
(伴隨矩陣)、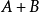 均正定;
均正定;
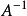
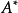
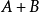
②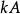 正定
正定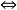
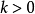 ;
;
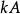
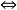
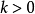
③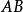 正定
正定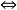
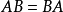
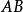
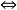
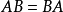
判定方法
判定二次型(或對稱矩陣)為正定的方法有如下兩種
行列式法
對於給定的二次型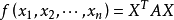 ,寫出它的矩陣,根據對稱矩陣的所有順序主子式是否全大於零來判定二次型 (或對稱矩陣)的正定性。
,寫出它的矩陣,根據對稱矩陣的所有順序主子式是否全大於零來判定二次型 (或對稱矩陣)的正定性。
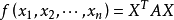
正慣性指數法
對於給定的二次型 ,先將化為標準形,然後根據標準形中平方項係數為正的個數是否等於 來判定二次型的正定性。
來判定二次型的正定性。

通過正交變換,將二次型化為標準形後,標準形中平方項的係數就是二次型矩陣的特徵值。因此,可先求二次型矩陣的特徵值,然後根據大於零的特徵值個數是否等於 來判定二次型的正定性。
來判定二次型的正定性。