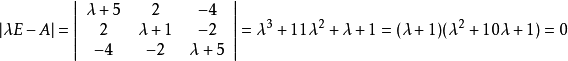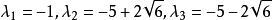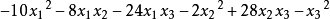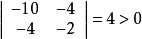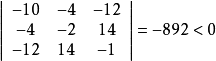實對稱矩陣A是負定的,如果二次型f(x1,x2,...,xn)=X'AX負定。矩陣負定的充分必要條件是它的特徵值都小於零。若矩陣A是n階負定矩陣,則A的偶數階順序主子式大於 0,奇數階順序主子式小於 0。
負定矩陣是矩陣類中的一種特殊矩陣,它在矩陣理論中占有重要地位。負定矩陣可以看成是與正定矩陣對應的概念,負定矩陣與正定矩陣有著許多相似的性質。
基本介紹
- 中文名:負定矩陣
- 外文名:negative definite matrix
- 學科:線性代數
- 相關:正定矩陣
- 常用判定:它的特徵值都小於零
- 意義:在矩陣理論中占有重要地位
意義
定義

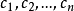
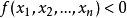


性質
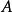

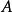


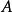
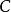

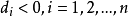
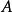


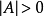

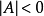
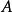

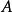
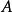
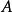
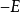
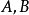

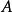
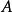
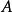
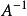
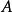
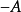
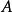

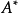

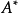
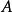
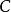
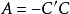
判定定理
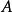
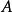

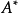

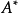
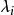
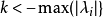
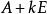
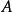

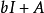
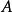

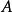

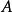
例題