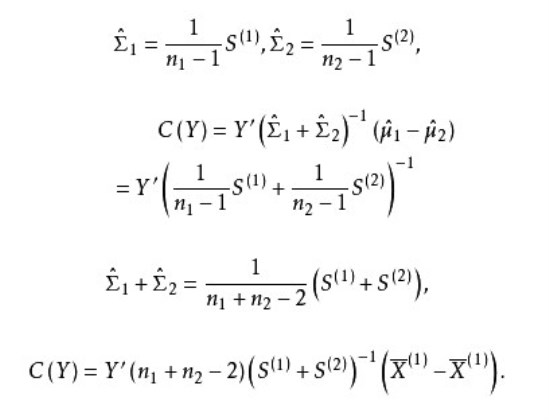Fisher判別法是判別分析的方法之一，它是藉助於方差分析的思想，利用已知各總體抽取的樣品的p維觀察值構造一個或多個線性判別函式y=l′x其中l= (l1，l2…lp)′，x= (x1，x2，…，xp)′，使不同總體之間的離差(記為B)儘可能地大，而同一總體內的離差(記為E)儘可能地小來確定判別係數l=(l1，l2…lp)′。數學上證明判別係數l恰好是|B-λE|=0的特徵根，記為λ1≥λ2≥…≥λr>0。所對應的特徵向量記為l1，l2，…lr，則可寫出多個相應的線性判別函式，在有些問題中，僅用一個λ1對應的特徵向量l1所構成線性判別函式y1=l′1x不能很好區分各個總體時，可取λ2對應的特徵向量l′2建立第二個線性判別函式y2=l′2x，如還不夠，依此類推。有了判別函式，再人為規定一個分類原則(有加權法和不加權法等)就可對新樣品x判別所屬。
基本介紹
- 中文名：Fisher判別法
- 所屬學科：數學
- 所屬問題：統計學（多元統計分析）
- 別名：費歇判別法
- 基本思想：方差思想
- 簡介：能較好區分各個總體的線性判別法
- 提出者：Fisher
- 提出時間：1936年
- 特點：對總體的分布不做任何要求
基本介紹,兩個總體的Fisher判別函式,多個總體的Fisher判別函式,判別規則,
基本介紹
Fisher判別法是根據方差分析的思想建立起來的一種能較好區分各個總體的線性判別法，由Fisher在1936年提出。該判別方法對總體的分布不做任何要求。
Fisher判別法是一種投影方法，把高維空間的點向低維空間投影。在原來的坐標系下，可能很難把樣品分開，而投影后可能區別明顯。一般說，可以先投影到一維空間(直線)上，如果效果不理想，在投影到另一條直線上(從而構成二維空間)，依此類推。每個投影可以建立一個判別函式。
下面給出Fisher判別法的詳細步驟。
兩個總體的Fisher判別函式
從兩個總體中抽取具有p個指標的樣品觀測數據，藉助於方差分析的思想構造一個線性判別函式：
當建立了判別式以後，對一個新的樣品值，我們可以將他的p個指標值代人判別式中求出Y值，然後與判別臨界值比較，就可以將該樣品歸類。設有2個總體
，其均值和協方差矩陣分別是
和
。可以證明，Fisher判別函式係數
若總體均值與方差未知，可通過樣本進行估計。
設從第一個總體
取得
個樣本，從第二個總體
取得
個樣本，記兩組樣本均值分別為
，樣本離差陣為
。顯然，的無偏估計為
。
的估計有兩種方式。
第一種估計方式是分別估計
當
時，兩種方法是等價的；當
與
相差不大時，兩種方法近似；當與相差很大時兩種方法相差較遠。目前採用較多的是第二種方法。
