解向量是線性方程組的一個解。因為一組解在空間幾何里可以表示為一個向量,所以叫做解向量。解向量在矩陣和線性方程組中是常用概念。如果n元齊次線性方程組Ax=0的係數矩陣的秩R(A)=r<n,則解空間S的基礎解系存在,且每個基礎解系恰有n-r個解向量。
基本介紹
- 中文名:解向量
- 外文名:solution vector
- 套用學科:數學術語
- 範疇:數理科學
- 定義:線性方程組的一個解
- 涉及:齊次線性方程組
概念
基本原理



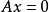
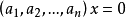

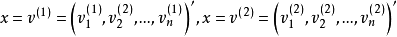





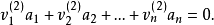
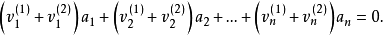
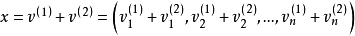



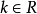


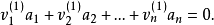
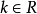





解向量是線性方程組的一個解。因為一組解在空間幾何里可以表示為一個向量,所以叫做解向量。解向量在矩陣和線性方程組中是常用概念。如果n元齊次線性方程組Ax=0的係數矩陣的秩R(A)=r<n,則解空間S的基礎解系存在,且每個基礎解系恰有n-r個解向量。



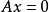
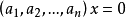

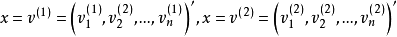





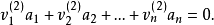
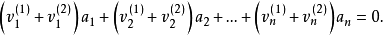
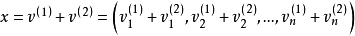



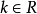


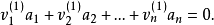
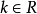




解向量是線性方程組的一個解。因為一組解在空間幾何里可以表示為一個向量,所以叫做解向量。解向量在矩陣和線性方程組中是常用概念。如果n元齊次線性方程組Ax=0的...
本書以專題的形式對高中數學中向繭的重點、難點進行了歸納、總結,涵蓋面廣,內容豐富,可使學生深入地理解向量的概念,靈活使用解題方法,可較大程度地提高學生在各類...
用解向量法解二元一次方程組此題中, , , , , , ,∴方程組有解,解為參考資料 1. 二元一次方程 .中文百科[引用日期2013-04-18] 2. 二元一次方程組 ....
假設對一模式,已抽取d個特徵,表示為x=(x1,x2,...,xd)T。x是d維空間的一個向量。模式識別問題就是根據模式的d個特徵來判別模式屬於w1,w2..,wc類中的...
例題:用解向量法解二元一次方程組此題中,a=3,b=1,c=4,d=2,e=2,f=0,ad-bc=3*2-1*4=2≠0∴方程組有解,解為x=(de-bf)/(ad-bc)=(2*2-1...
4.2 線性方程組解的結構與解的求法4.3 含參數的線性方程組的解法4.4 基礎解系的證法4.5 解向量的證法4.6 抽象線性方程組的求解...
這種方法的基本思路是,利用初始平差的解向量(接收機點的坐標及整周未知數的實數解)及其精度信息(單位權中誤差和方差協方差陣),以數理統計理論的參數估計和統計...
設A 是n階方陣,如果存在數m和非零n維列向量 x,使得 Ax=mx 成立,則稱 m 是矩陣A的一個特徵值(characteristic value)或本徵值(eigenvalue)。...
4.理解非齊次線性方程組解的結構及通解的概念.5.掌握用初等行變換求解線性方程組的方法.矩陣的特徵值和特徵向量考試要求1.理解矩陣的特徵值、特徵向量的概念,掌握...
第51題 向量的線性運算及幾何意義是什麼?第52題 向量的數量積運算有什麼技巧?第53題 怎樣解向量平行問題?第54題 怎樣解向量垂直問題?...
《新編中學數學解題方法全書(高中版下卷)(3)》內容包括函式、數列、向量、三角...向量表示 怎樣用基向量法求空間的角 怎樣數形結合求解平面向量問題 怎樣解向量...
