矩陣圖法,是利用數學上矩陣的形式表示因素間的相互關係,從中探索問題所在並得出解決問題的構想。它是進行多元思考,分析問題的方法。矩陣圖法就是從多維問題的事件中,找出成對的因素,排列成矩陣圖,然後根據矩陣圖來分析問題,確定關鍵點的方法,它是一種通過多因素綜合思考,探索問題的好方法。在複雜的質量問題中,往往存在許多成對的質量因素,將這些成對因素找出來,分別排列成行和列,其交點就是其相互關聯的程度,在此基礎上再找出存在的問題及問題的形態,從而找到解決問題的思路。
基本介紹
- 中文名: 矩陣圖法
- 外文名:Matrix Diagram
- 套用類型:質量管理
- 學科類型:數學
簡介,製作步驟,類型,用途,相關連結,
簡介
矩陣圖法(Matrix Diagram)
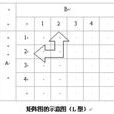
矩陣圖的形式如下圖所示,A為某一個因素群,a1、a2、a3、a4、…是屬於A這個因素群的具體因素,將它們排列成行;B為另一個因素群,b1、 b2、b3、b4、…為屬於B這個因素群的具體因素,將它們排列成列;行和列的交點表示A和B各因素之間的關係,按照交點上行和列因素是否相關聯及其關聯程度的大小,可以探索問題的所在和問題的形態,也可以從中得到解決問題的啟示等。 GE矩陣圖法
GE矩陣圖法
 GE矩陣圖法
GE矩陣圖法質量管理中所使用的矩陣圖,其成對因素往往是要著重分析的質量問題的兩個側面,如生產過程中出現了不合格時,著重需要分析不合格的現象和不合格的原因之間的關係,為此,需要把所有缺陷形式和造成這些缺陷的原因都羅列出來,逐一分析具體現象與具體原因之間的關係,這些具體現象和具體原因分別構成矩陣圖中的行元素和列元素。
矩陣圖的最大優點在於,尋找對應元素的交點很方便,而且不會遺漏,顯示對應元素的關係也很清楚。矩陣圖法還具有以下幾個特點:
①可用於分析成對的影響因素;
②因素之間的關係清晰明了,便於確定重點;
③便於與系統圖結合使用。
製作步驟
製作矩陣圖一般要遵循以下幾個步驟:
①列出質量因素;
②把成對因素排列成行和列,表示其對應關係;
③選擇合適的矩陣圖類型;
④在成對因素交點處表示其關係程度,一般憑經驗進行定性判斷,可分為三種:關係密切、關係較密切、關係一般(或可能有關係),並用不同符號表示;
⑤根據關係程度確定必須控制的重點因素;
⑥針對重點因素作對策表。
類型
矩陣圖法在套用上的一個重要特徵,就是把應該分析的對象表示在適當的矩陣圖上。因此,可以把若干種矩陣圖進行分類,表示出他們的形狀,按對象選擇並靈活運用適當的矩陣圖形。常見的矩陣圖有以下幾種:
(1)L型矩陣圖。是把一對現象用以矩陣的行和列排列的二元表的形式來表達的一種矩陣圖,它適用於若干目的與手段的對應關係,或若干結果和原因之間的關係。

(2)T型矩陣圖。是A、B兩因素的L型矩陣和A、C兩因素的L型矩陣圖的組合矩陣圖,這種矩陣圖可以用於分析質量問題中"不良現象一原因一工序"之間的關係,也可以用於分析探索材料新用途的"材料成分一特性一用途"之間的關係等。

(3)Y型矩陣圖。是把A因素與B因素、B因素與C因素、C因素與A因素三個L型矩陣圖組合在一起而形成的矩陣圖。

(4)X型矩陣圖。是把A因素與B因素、B因素與C因素、C因素與D因素、D因素與A因素四個L型矩陣圖組合而形成的矩陣圖,這種矩陣圖表示A和 B、D,B和A、C,C和B、D,D和A、C這四對因素間的相互關係,如"管理機能一管理項目一輸入信息一輸出信息"就屬於這種類型。

(5)C型矩陣圖。是以A、B、C三因素為邊做出的六面體,其特徵是以A、B、C三因素所確定的三維空間上的點為"著眼點"。

(6)P型矩陣圖。

用途
矩陣圖法的用途十分廣泛,在質量管理中,常用矩陣圖法解決以下問題:
①把系列產品的硬體功能和軟體功能相對應,並要從中找出研製新產品或改進老產品的切入點;
②明確應保證的產品質量特性及其與管理機構或保證部門的關係,使質量保證體制更可靠;
③明確產品的質量特性與試驗測定項目、試驗測定儀器之間的關係,力求強化質量評價體制或使之提高效率;
④當生產工序中存在多種不良現象,且它們具有若干個共同的原因時,希望搞清這些不良現象及其產生原因的相互關係,進而把這些不良現象一舉消除;
⑤在進行多變數分析、研究從何處入手以及以什麼方式收集數據。