設點P滿足OP=(1-t)OA+tOB，則AP=tAB，即P在直線L上，其中實數t叫做參變數，簡稱參數。對直線L上任意一點P，一定存在唯一的實數t滿足該向量等式；反之，對每一個實數t，在直線L上都有唯一的一個點P與之對應。
基本介紹
- 中文名：向量參數方程式
- 別稱：向量參數方程
- 表達式：OP=(1-t)OA+tOB
- 適用領域範圍：高中數學
- 改進者：朱天龍
- 改進時間：2017年
定律定義,推導過程,公式改進,改進優劣,典型例題,
定律定義
設點P滿足OP=(1-t)OA+tOB，則AP=tAB，即P在直線L上，其中實數t叫做參變數，簡稱參數。對直線L上任意一點P，一定存在唯一的實數t滿足該向量等式；反之，對每一個實數t，在直線L上都有唯一的一個點P與之對應。
推導過程
設點P在直線L上，則由平行向量基本定理可知，存在實數t，使
AP=tAB=t(OB-OA)
所以
OP=OA+AP=OA+tOB-tOA=(1-t)OA+tOB(1-1)
由此可見，對直線L上任意一點P，一定存在唯一的實數t滿足該向量等式；反之，對每一個實數t，在直線L上都有唯一的一個點P與之對應。
因此，該向量等式叫做直線L的向量參數方程式，其中實數t叫做參變數，簡稱參數。
特別的，當t=
時，點P是AB中點，即
OM= (OA+OB)(1-2)
這是線段AB中點的向量表達式。
當OP=(x0,y0), OA=(x1,y1) OB=(x2,y2)時，
公式(1-1)可變形為：
(x0,y0)=(1-t)(x1,y1)+t(x2,y2) (1-3)
該公式即為定比分點坐標公式。
公式改進
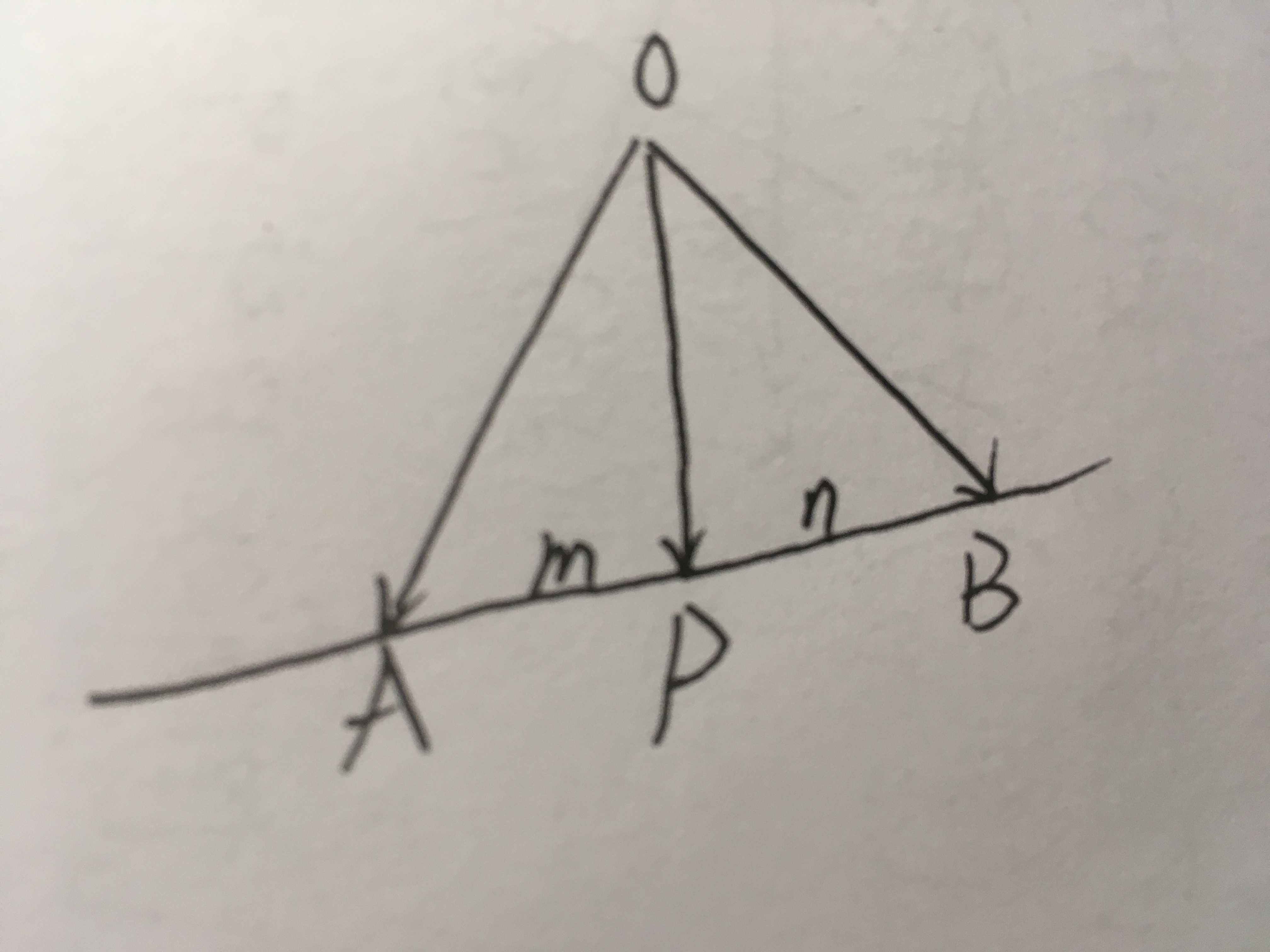
當P在AB線段上時，設PA=m，PB=n，則此時t=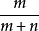
,又1-t=
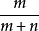
於是，公式(1-1)變為
OP= OA+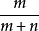 OB (1-4)
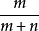
公式(1-3)變為
(x0,y0)= (x1,y1)+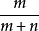 (x2,y2) (1-5)
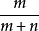
改進優劣
優勢：公式(1-4)(1-5)相比較於公式(1-1)(1-3)具有高度對稱性，且不需要計算實數t，進一步降低學生學習難度，有利於公式的套用，大幅度降低錯誤率。
劣勢：該兩組公式僅適用於點P線上段AB上的情況，當其在AB延長線上時，需要用OA,OP表示OB，進而解出OP，另一情況下也需要進行求解。
評價：提高了計算準確率，降低了公式難度，但卻增加了計算量，不過好在計算量很小。
典型例題
例一：如圖所示，P為線段AB上靠近A的一個三等分點， 則套用公式(1-4)可知：m=1，n=2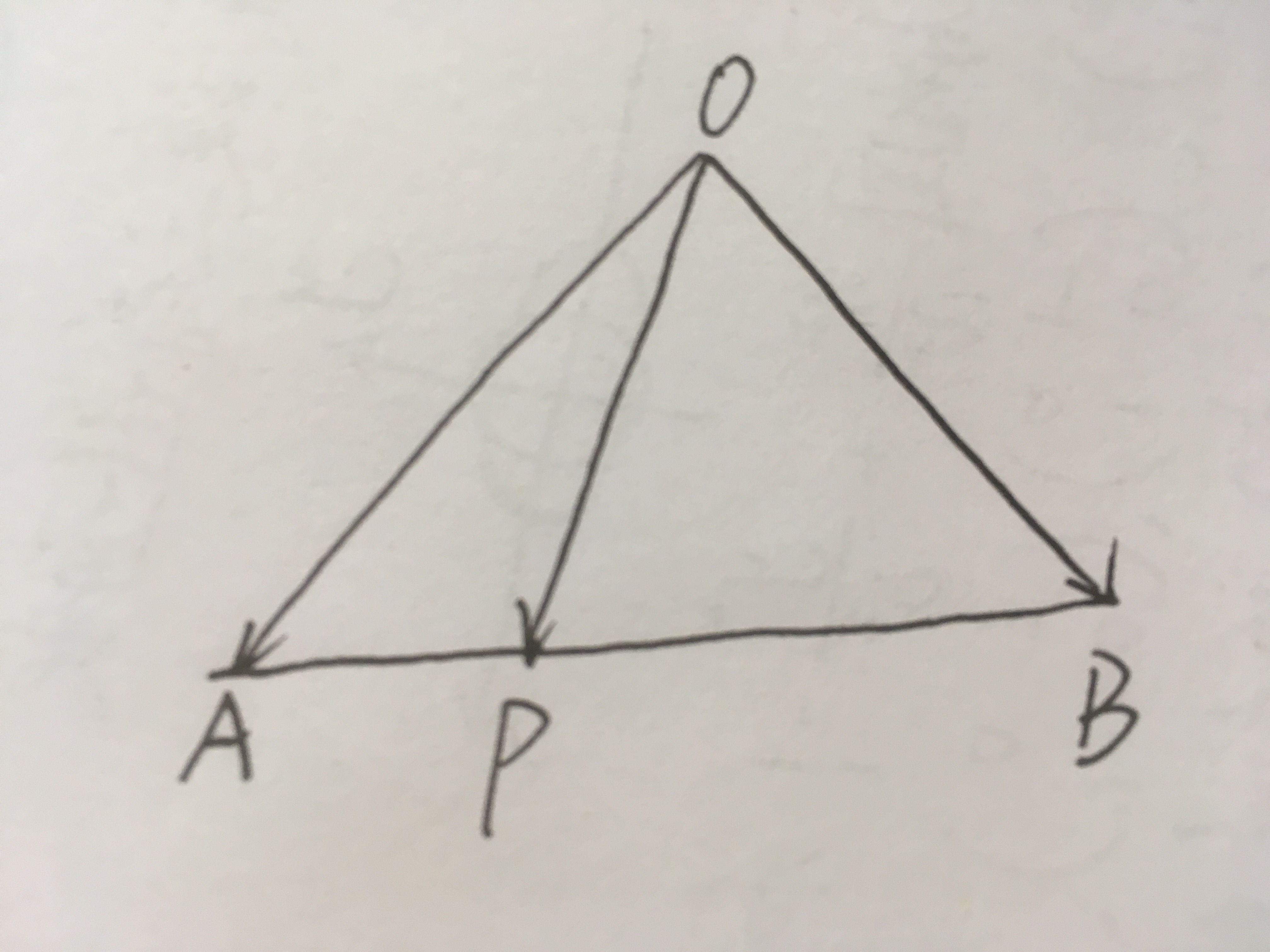
於是OP= OA+ OB= 
OA+
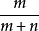OB
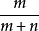
例二：如圖所示，P為AB延長線上任意一點，且BP=2AB，
已知A(-3,3), B(3,6)，設AB=m=1，BP=n=2
於是(xB,yB)= (xA,yA)+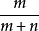 (xP,yP)
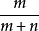
=(-3,3)+(xP,yP)=(3,6)
解得P(15,12)
