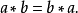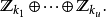基本介紹
定義,符號,乘法表,歷史註記,性質,例子,有限阿貝爾群,相關條目,
定義
因為阿貝爾群的群運算滿足交換律和結合律，群元素乘積的值與乘法運算時的次序無關。而群運算不滿足交換律的群被稱為“非阿貝爾群”，或“非交換群”。
符號
阿貝爾群有兩種主要運算符號—加法和乘法。
| 約定 | 運算 | 單位元 | 冪 | 逆元 |
|---|---|---|---|---|
| 加法運算 | x+y | 0 | nx | −x |
| 乘法運算 | x*y或xy | e或1 | xn | x-1 |
一般地說，乘法符號是群的常用符號，而加法符號是模的常用符號。當同時考慮阿貝爾群和非阿貝爾群時，加法符號還可以用來強調阿貝爾群是特定群。
乘法表
驗證有限群是阿貝爾群，可以構造類似乘法表的一種表格（矩陣），它稱為凱萊表。如果群G= {g1=e,g2, ...,gn}在運算⋅下，則這個表的第(i,j)個表項包含乘積gi⋅gj。群是阿貝爾群若且唯若這個表是關於主對角線是對稱的（就是說這個矩陣是對稱矩陣）。
這是成立的因為如果它是於阿貝爾群，則gi⋅gj=gj⋅gi。這蘊含了第(i,j)個表項等於第(j,i)個表項，就是說這個表示關於主對角線對稱的。
歷史註記
阿貝爾群是Camille Jordan以挪威數學家尼爾斯·阿貝爾命名的，他首先察覺到了阿貝爾首先發表的這種群與根式可解性的聯繫的重要性。
性質
如果n是自然數而x是使用加號的阿貝爾群G的一個元素，則nx可以定義為x+x+ ... +x（n個數相加）並且（−n）x= −（nx）。以這種方式，G變成在整數的環Z上的模。事實上，在Z上的模都可以被識別為阿貝爾群。
關於阿貝爾群（比如在主理想整環Z上的模）的定理經常可以推廣到在任意主理想整環上的模。典型的例子是有限生成阿貝爾群的分類是在主理想整環上的有限生成模的結構定理的特殊情況。在有限生成阿貝爾群的情況下，這個定理保證阿貝爾群可以分解為撓群和自由阿貝爾群的直和。前者可以被寫為形如Z/pkZ對於素數p的有限多個群的直和，而後者是有限多個Z的複本的直和。
如果f,g:G→H是在阿貝爾群之間的兩個群同態，則它們的和f+g，定義為(f+g)(x) =f(x) +g(x)，也是阿貝爾同態。（如果H是非阿貝爾群則這就不成立。）所有從G到H的群同態的集合Hom(G,H)因此是自身方式下的阿貝爾群。
例子
- 整數集和加法運算"+"是阿貝爾群，指示為(Z,+)，運算 +組合兩個整數形成第三個整數，加法是符合結合律的，零是加法單位元，所有整數n都有加法逆元−n，加法運算是符合交換律的因為對於任何兩個整數m和n有m+n=n+m。
- 所有循環群G是阿貝爾群，因為如果x,y在G中，則xy=aman=am+n=an+m=anam=yx。因此整數集Z形成了在加法下的阿貝爾群，整數模以nZ/nZ也是。
- 所有環都是關於它的加法運算的阿貝爾群。在交換環中的可逆元形成了阿貝爾乘法群。特別是實數集是在加法下的阿貝爾群，非零實數集在乘法下是阿貝爾群。
- 所有阿貝爾群的子群都是正規子群，所以每個子群都引發商群。阿貝爾群的子群、商群和直和也是阿貝爾群。
有限阿貝爾群
整數模以n的循環群Z/nZ是最常見的群的例子。已證實了任意有限阿貝爾群都同構於素數階的有限循環群的直和，並且這些階數是唯一確定的，形成了一個不變數（invariant）的完備系統。有限阿貝爾群的自同構群可以依據這些不變數來直接描述。有關理論最初發展自費迪南德·格奧爾格·弗羅貝尼烏斯和Ludwig Stickelberger在1879年的論文，後來被簡化和推廣到在主理想整環上的有限生成模，形成了線性代數的一個重要組成部分。
