阿貝爾積分,其中R(x,y)是x和y的有理函式,且存在二元多項式ƒ,使ƒ(x,y)=0。他還證明了關於上述積分之和的定理,現稱阿貝爾定理。
基本介紹
- 中文名:阿貝爾積分方程
- 外文名:Abel integral equation
- 提出者:阿貝爾,N.H.
- 套用學科:數學
定義
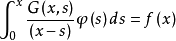
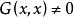

阿貝爾積分,其中R(x,y)是x和y的有理函式,且存在二元多項式ƒ,使ƒ(x,y)=0。他還證明了關於上述積分之和的定理,現稱阿貝爾定理。
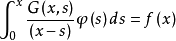
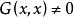
阿貝爾積分,其中R(x,y)是x和y的有理函式,且存在二元多項式ƒ,使ƒ(x,y)=0。他還證明了關於上述積分之和的定理,現稱阿貝爾定理。...
阿貝爾積分運算元是由阿貝爾積分方程導出的運算元。...... 阿貝爾積分運算元是由阿貝爾積分方程導出的運算元。阿貝爾積分運算元(Abel integral operator)由阿貝爾積分方程導出的運算元....
阿貝爾函式方程(Abel functional equation)是施洛德函式方程的一種變形方程。該方程是由阿貝爾首先提出。阿貝爾是挪威數學家。生於挪威西南海岸斯塔萬格附近的小島芬島(...
積分方程是含有對未知函式的積分運算的方程,與微分方程相對。許多數學物理問題需通過積分方程或微分方程求解。積分方程是近代數學的一個重要分支。數學、自然科學和工程...
阿貝爾微分是一類微分式。閉黎曼曲面k上的亞純微分稱為阿貝爾微分。阿貝爾微分分...設S 是任意緊黎曼面,其上有滿足不可約代數方程 的亞純函式 z 和ω,那么 S...
阿貝爾從理論上予以證明,無論怎樣用加、減、乘、除及開方運算,無論將方程的係數怎樣排列,它都決不可能是一般五次方程的求根公式。...
但他的窮困及病況並沒有減低他對數學的熱誠,他在這段期間寫了大量的論文,主要是方程理論及橢圓函式,也就是有關阿貝爾方程和阿貝爾群的理論。他比雅可比(Jacobi)...
第1卷 (1826)刊登了7篇阿貝爾的文章,其中有一般五次方程用根式不能求解的證明。以後各卷也有很多他的文章。1826年阿貝爾到巴黎,遇見了A.-M.勒讓德和A.-L....
初等常微分方程,能用微積分的方法求出其通解或通積分的常微分方程。...... 當有個特解為已知時,它是可積分的。③第一類阿貝爾方程和第二類阿貝爾方程它們也有不...
本書的主講對象是挪威著名數學家阿貝爾,他的主要貢獻在於研究了二項式定理,並成功求解了五次方程,為世界數學領域的代數問題成功增添了新內容。本書講述了阿貝爾從出生...
