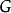
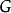
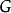
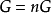
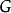
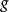
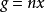
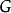
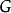
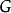
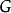
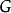
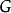
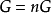
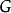
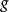
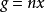
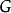
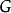
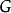
可除阿貝爾群(divisible abelian group)是阿貝爾群理論中的一個重要概念. 設 
是一個阿貝爾群（運算表為加法），
是一個正整數，考慮 的如下子集
可除阿貝爾群
相關詞條
- 可除阿貝爾群
可除阿貝爾群(divisible abelian group)是阿貝爾群理論中的一個重要概念. 設 是一個阿貝爾群(運算表為加法), 是一個正整數,考慮 的如下子集 易見它是 ...
- 阿貝爾群
阿貝爾群(Abelian Group),又稱交換群或加群,是這樣一類群:它由自身的集合 G 和二元運算 * 構成。它除了滿足一般的群公理,即運算的結合律、G 有單位元、所有 ...
- 可除模
可除模(divisible module)是一類重要的模。可除阿貝爾群的推廣。內射模一定是可除模,反之不一定成立。模是一個重要的代數系統。它是一個帶運算元區A的交換(加)...
- 亞阿貝爾群
亞阿貝爾群(metAbelian group)是一種可解群。指導出列長度至多為2的群。設G是群,若G有導出列 ,則稱G為亞阿貝爾群。設G是群,若G有循環的正規子群N,使得G...
- 初等阿貝爾群
在群論中,初等阿貝爾群是有限阿貝爾群,這裡的所有非平凡元素都有 p 階而 p 是素數。...
- 混合阿貝爾群
混合阿貝爾群(mixed Abelian group)一種常見的阿貝爾群.設群G是阿貝爾群.若G既包含非平九的有限階元素又包含無限階元素,則稱G是混合阿貝爾群.混合阿貝爾群的最初...
- 無扭阿貝爾群
無扭阿貝爾群(torsion-free Abelian group)重要的阿貝爾群之一不含有限階元素的阿貝爾群稱為無扭阿貝爾群.它比準素阿貝爾群要難處理得多,實際上除了秩為1的這樣...
- 準素阿貝爾群
準素阿貝爾群(primary Abelian group)是一種最重要的周期阿貝爾群,準素阿貝爾群的理論是阿貝爾群的一般理論中最豐富和最深人的幾個分支之一。...
- 阿貝爾群機器
介紹 阿貝爾群機器(Abelian group machine)一種建立在阿貝爾群上的形式系統.這時系統可定義為藝=(U,X,Y,占,月),式中U,X,Y都是阿貝爾群,且有三個同態 F:X...
- 阿貝爾擴張
阿貝爾擴張(Abelian extension)是一類重要的域擴張,設K是域F的伽羅瓦擴域,若其伽羅瓦群G(K/F)為一阿貝爾群,則稱此擴張為阿貝爾擴張,此時,K稱為F上阿貝爾擴域...
- 阿貝爾積分方程
阿貝爾積分,其中R(x,y)是x和y的有理函式,且存在二元多項式ƒ,使ƒ(x,y)=0。他還證明了關於上述積分之和的定理,現稱阿貝爾定理。...
- 群(數學概念)
在數學中,群表示一個擁有滿足封閉性、結合律、有單位元、有逆元的二元運算的代數結構,包括阿貝爾群、同態和共軛類。...
- 平凡群
在數學裡,平凡群是指一個只包含單一元素e的群,其群運算只有e + e = e,單位元素平凡是e,且為阿貝爾群;這些結果都是平凡的,因此以此命名。...
- 克萊因四元群
有4個元素,除單位元外其階均為2。 克萊因四元群通常以V表示或K4表示,意為Z2×Z2,(來自德文的四元群Vierergruppe)。它也是阿貝爾群,就是2階的循環群與...
- 有序群
1770年,拉格朗日在討論代數方程根之間的置換時,首先引入群的概念,而它的名稱,是伽羅華在1830年首先提出的。有序群交換群 編輯 交換群亦稱阿貝爾群,是一種重要的群...
- 有效除子
具體地,若D表示X中不含於X的奇異軌跡之中且余維數為1的不可約子簇的全體,Div(X)表示以D為基的自由阿貝爾群,則Div(X)中的元稱為除子。設A=∑niAi是一...
- 代數數理論講義
§21. 代數整數的定義,可除性與單位 §22. 域的整數作為一個阿貝爾群:域的基與判別式 §23. K(5)中整數的分解:不屬於域的最大公因子 §24. 理想的定義...
- 加性範疇
阿貝爾群範疇、環R上的R模範疇都是阿貝爾範疇。阿貝爾範疇具有加性範疇的一切性質。阿貝爾範疇的對偶範疇仍為阿貝爾範疇。阿貝爾範疇中既單且滿的態射是單位態射。...
