數學是中國古代科學中一門重要的學科,它的歷史悠久,成就輝煌。根據它本身發展的特點,可以分為五個時期:
①中國古代數學的萌芽;
②中國古代數學體系的形成;
③中國古代數學的發展;
④中國古代數學的繁榮;
⑤中西方數學的融合。
基本介紹
- 中文名:中國數學史
- 外文名:History of Chinese mathematics
中國數學發展長河,萌芽階段,體系形成,數學發展,數學繁榮,中西融合,發展衰落,相關信息,高次方程,內插法,勾股解法,弧矢割圓術,縱橫圖,中國數學特點,其他相關信息,西方數學,現代數學,
中國數學發展長河
萌芽階段
中國古代數學的萌芽原始公社末期,私有制和貨物交換產生以後,數與形的概念有了進一步的發展,仰韶文化時期出土的陶器,上面已刻有表示1234的符號。到原始公社末期,已開始用文字元號取代結繩記事了。
西安半坡出土的陶器有用1~8個圓點組成的等邊三角形和分正方形為100個小正方形的圖案,半坡遺址的房屋基址都是圓形和方形。為了畫圓作方,確定平直,人們還創造了規、矩、準、繩等作圖與測量工具。據《史記·夏本紀》記載,夏禹治水時已使用了這些工具。
起源
據《易.繫辭》記載:“上古結繩而治,後世聖人易之以書契”。甲骨文卜辭中有很多記數的文字。從一到十,及百、千、萬是專用的記數文字,共有13個獨立符號,記數用合文書寫,其中有十進制制的記數法,出現最大的數字為三萬。算籌是中國古代的計算工具,而這種計算方法稱為籌算。算籌的產生年代已不可考,但可以肯定的是籌算在春秋時代已很普遍。
用算籌記數,有縱、橫兩種方式:
表示一個多位數字時,採用十進位值制,各位值的數目從左到右排列,縱橫相間〔法則是:一縱十橫,百立千僵,千、十相望,萬、百相當〕,並以空位表示零。算籌為加、減、乘、除等運算建立起良好的條件。
在幾何學方面《史記.夏本記》中說大禹治水時已使用了規、矩、準、繩等作圖和測量工具,並早已發現“勾三股四弦五”這個勾股定理〔西方稱勾股定理〕的特例。戰國時期,齊國人著的《考工記》匯總了當時手工業技術的規範,包含了一些測量的內容,並涉及到一些幾何知識,例如角的概念。
商朝時代
商代中期,在甲骨文中已產生一套十進制數字和記數法,其中最大的數字為三萬;與此同時,殷人用十個天干和十二個地支組成甲子、乙丑、丙寅、丁卯等60個名稱來記60天的日期;在周代,又把以前用陰、陽符號構成的八卦表示八種事物發展為六十四卦,表示64種事物。
公元前一世紀的《周髀算經》提到西周初期用矩測量高、深、廣、遠的方法,並舉出勾股形的勾三、股四、弦五以及環矩可以為圓等例子。《禮記·內則》篇提到西周貴族子弟從九歲開始便要學習數目和記數方法,他們要受禮、樂、射、馭、書、數的訓練,作為“六藝”之一的數已經開始成為專門的課程。 祖沖之
祖沖之
 祖沖之
祖沖之春秋戰國
春秋戰國之際,籌算已得到普遍的套用,籌算記數法已使用十進位值制,這種記數法對世界數學的發展是有劃時代意義的。這個時期的測量數學在生產上有了廣泛套用,在數學上亦有相應的提高。
戰國時期的百家爭鳴也促進了數學的發展,尤其是對於正名和一些命題的爭論直接與數學有關。名家認為經過抽象以後的名詞概念與它們原來的實體不同,他們提出“矩不方,規不可以為圓”,把“大一”(無窮大)定義為“至大無外”,“小一”(無窮小)定義為“至小無內”。還提出了“一尺之棰,日取其半,萬世不竭”等命題。
墨家
而墨家則認為名來源於物,名可以從不同方面和不同深度反映物。墨家給出一些數學定義。例如圓、方、平、直、次(相切)、端(點)等等。
名家的命題論述了有限長度可分割成一個無窮序列,墨家的命題則指出了這種無限分割的變化和結果。名家和墨家的數學定義和數學命題的討論,對中國古代數學理論的發展是很有意義的。
體系形成
《九章算術》是戰國、秦、漢封建社會創立並鞏固時期數學發展的總結,就其數學成就來說,堪稱是世界數學名著。例如分數四則運算、今有術(西方稱三率法)、開平方與開立方(包括二次方程數值解法)、盈不足術(西方稱雙設法)、各種面積和體積公式、線性方程組解法、正負數運算的加減法則、勾股形解法(特別是勾股定理和求勾股數的方法)等,水平都是很高的。其中方程組解法和正負數加減法則在世界數學發展上是遙遙領先的。就其特點來說,它形成了一個以籌算為中心、與古希臘數學完全不同的獨立體系。 中國數學史
中國數學史
 中國數學史
中國數學史《九章算術》有幾個顯著的特點:採用按類分章的數學問題集的形式;算式都是從籌算記數法發展起來的;以算術、代數為主,很少涉及圖形性質;重視套用,缺乏理論闡述等。
秦漢時期強調數學的套用性。成書於東漢初年的《九章算術》,排除了戰國時期在百家爭鳴中出現的名家和墨家重視名詞定義與邏輯的討論,偏重於與當時生產、生活密切相結合的數學問題及其解法。
數學發展
魏晉時期
東晉以後
東晉以後,中國長期處於戰爭和南北分裂的狀態。祖沖之父子的工作就是經濟文化南移以後,南方數學發展的具有代表性的工作,他們在劉徽注《九章算術》的基礎上,把傳統數學大大向前推進了一步。他們的數學工作主要有:計算出圓周率在3.1415926~3.1415927之間;提出祖暅原理;提出二次與三次方程的解法等。 考古發現
考古發現
 考古發現
考古發現據推測,祖沖之在劉徽割圓術的基礎上,算出圓內接正6144邊形和正12288邊形的面積,從而得到了這個結果。他又用新的方法得到圓周率兩個分數值,即約率22/7和密率355/113。祖沖之這一工作,使中國在圓周率計算方面,比西方領先約一千年之久;
祖沖之之子祖暅總結了劉徽的有關工作,提出“冪勢既同則積不容異”,即等高的兩立體,若其任意高處的水平截面積相等,則這兩立體體積相等,這就是著名的祖暅公理。祖暅套用這個公理,解決了劉徽尚未解決的球體積公式。
隋唐朝時期
隋煬帝大興土木,客觀上促進了數學的發展。唐初王孝通的《緝古算經》,主要討論土木工程中計算土方、工程分工、驗收以及倉庫和地窖的計算問題,反映了這個時期數學的情況。王孝通在不用數學符號的情況下,立出數字三次方程,不僅解決了當時社會的需要,也為後來天元術的建立打下基礎。此外,對傳統的勾股形解法,王孝通也是用數字三次方程解決的。
唐初統治者繼承隋制,656年在國子監設立算學館,設有算學博士和助教,學生30人。由太史令李淳風等編纂注釋《算經十書》,作為算學館學生用的課本,明算科考試亦以這些算書為準。李淳風等編纂的《算經十書》,對保存數學經典著作、為數學研究提供文獻資料方面是很有意義的。他們給《周髀算經》、《九章算術》以及《海島算經》所作的註解,對讀者是有幫助的。隋唐時期,由於曆法的需要,天算學家創立了二次函式的內插法,豐富了中國古代數學的內容。
算籌是中國古代的主要計算工具,它具有簡單、形象、具體等優點,但也存在布籌占用面積大,運籌速度加快時容易擺弄不正而造成錯誤等缺點,因此很早就開始進行改革。其中太乙算、兩儀算、三才算和珠算都是用珠的槽算盤,在技術上是重要的改革。尤其是“珠算”,它繼承了籌算五升十進與位值制的優點,又克服了籌算縱橫記數與置籌不便的缺點,優越性十分明顯。但由於當時乘除算法仍然不能在一個橫列中進行。算珠還沒有穿檔,攜帶不方便,因此仍沒有普遍套用。 九章算術
九章算術
 九章算術
九章算術唐中期以後,商業繁榮,數字計算增多,迫切要求改革計算方法,從《新唐書》等文獻留下來的算書書目,可以看出這次算法改革主要是簡化乘、除算法,唐代的算法改革使乘除法可以在一個橫列中進行運算,它既適用於籌算,也適用於珠算。
教育建立
隋朝大興土木,客觀上促進了數學的發展。唐初王孝通撰《緝古算經》,主要是通過土木工程中計算土方、工程的分工與驗收以及倉庫和地窖計算等實際問題,討論如何以幾何方式建立三次多項式方程,發展了《九章算術》中的少廣、勾股章中開方理論。
隋唐時期是中國封建官僚制度建立時期,隨著科舉制度與國子監製度的確立,數學教育有了長足的發展。656年國子監設立算學館,設有算學博士和助教,由太史令李淳風等人編纂注釋《算經十書》〔包括《周髀算經》、《九章算術》、《海島算經》、《孫子算經》、《張丘建算經》、《夏侯陽算經》、《緝古算經》、《五曹算經》、《五經算術》和《綴術》〕,作為算學館學生用的課本。對保存古代數學經典起了重要的作用。
由於南北朝時期的一些重大天文發現在隋唐之交開始落實到曆法編算中,使唐代曆法中出現一些重要的數學成果。公元600年,隋代劉焯在制訂《皇極曆》時,在世界上最早提出了等間距二次內插公式,這在數學史上是一項傑出的創造,唐代僧一行在其《大衍曆》中將其發展為不等間距二次內插公式。
唐朝後期,計算技術有了進一步的改進和普及,出現很多種實用算術書,對於乘除算法力求簡捷。
數學繁榮
北宋時期
960年,北宋的建立結束了五代十國割據的局面。北宋的農業、手工業、商業空前繁榮,科學技術突飛猛進,火藥、指南針、印刷術三大發明就是在這種經濟高漲的情況下得到廣泛套用。1084年秘書省第一次印刷出版了《算經十書》,1213年鮑擀之又進行翻刻。這些都為數學發展創造了良好的條件。
11世紀~14世紀
從11~14世紀約300年期間,出現了一批著名的數學家和數學著作,如賈憲的《黃帝九章算法細草》,劉益的《議古根源》,秦九韶的《數書九章》,李冶的《測圓海鏡》和《益古演段》,楊輝的《詳解九章算法》《日用算法》和《楊輝算法》,朱世傑的《算學啟蒙》《四元玉鑒》等,很多領域都達到古代數學的高峰,其中一些成就也是當時世界數學的高峰。 中國數學史
中國數學史
 中國數學史
中國數學史從開平方、開立方到四次以上的開方,在認識上是一個飛躍,實現這個飛躍的就是賈憲。楊輝在《九章算法纂類》中載有賈憲“增乘開平方法”、“增乘開立方法”;在《詳解九章算法》中載有賈憲的“開方作法本源”圖、“增乘方法求廉草”和用增乘開方法開四次方的例子。根據這些記錄可以確定賈憲已發現二項係數表,創造了增乘開方法。這兩項成就對整個宋元數學發生重大的影響,其中賈憲三角比西方的帕斯卡三角形早提出600多年。
秦九韶是高次方程解法的集大成者,為了適應增乘開方法的計算程式,奏九韶把常數項規定為負數,把高次方程解法分成各種類型。當方程的根為非整數時,秦九韶採取繼續求根的小數,或用減根變換方程各次冪的係數之和為分母,常數為分子來表示根的非整數部分,這是《九章算術》和劉徽注處理無理數方法的發展。在求根的第二位數時,秦九韶還提出以一次項係數除常數項為根的第二位數的試除法,這比西方最早的霍納方法早500多年。
朱世傑的四元高次聯立方程組表示法是在天元術的基礎上發展起來的,他把常數放在中央,四元的各次冪放在上、下、左、右四個方向上,其他各項放在四個象限中。朱世傑的最大貢獻是提出四元消元法,其方法是先擇一元為未知數,其他元組成的多項式作為這未知數的係數,列成若干個一元高次方程式,然後套用互乘相消法逐步消去這一未知數。重複這一步驟便可消去其他未知數,最後用增乘開方法求解。這是線性方法組解法的重大發展,比西方同類方法早400多年。
宋元時期
中國古代計算技術改革的高潮也是出現在宋元時期。宋元明的歷史文獻中載有大量這個時期的實用算術書目,其數量遠比唐代為多,改革的主要內容仍是乘除法。與算法改革的同時,穿珠算盤在北宋可能已出現。
宋元數學家都在不同程度上反對理學家的象數神秘主義。秦九韶雖曾主張數學與道學同出一源,但他後來認識到,“通神明”的數學是不存在的,只有“經世務類萬物”的數學;莫若在《四元玉鑒》序文中提出的“用假象真,以虛問實”則代表了高度抽象思維的思想方法;楊輝對縱橫圖結構進行研究,揭示出洛書的本質,有力地批判了象數神秘主義。所有這些,無疑是促進數學發展的重要因素。
中國古代計算技術改革的高潮也是出現在宋元時期。宋元明的歷史文獻中載有大量這個時期的實用算術書目,其數量遠比唐代為多。改革的主要內容仍是乘除法。“留頭乘”最早見於朱世傑《算學啟蒙》。“九歸”最早出現在沈括的《夢溪筆談》,楊輝在《乘除通變本末》(1274)、朱世傑在《算學啟蒙》中進一步把它完善。“歸除”最早見於《算學啟蒙》,“撞歸”、“起一”是朱世傑首先提出來的,丁巨(著有《丁巨算法》,1355)、何平予(著有《詳明算法》,1373)和賈亨(著有《算法全能集》)把它具體化。“留頭乘”與“歸除”的出現,使乘除法不需任何變通便可在一個橫列里進行,與現今珠算的方法完全一樣。與算法改革的同時,穿珠算盤在北宋已可能出現。但如果把現代珠算看成是既有穿珠算盤,又有一套完善的算法和口訣,那么應該說它最後完成於元代。 中國數學史
中國數學史
 中國數學史
中國數學史宋元數學的繁榮,是社會經濟發展和科學技術發展的必然結果,是傳統數學發展的必然結果。此外,數學家們的科學思想與數學思想也是十分重要的。宋元數學家都在不同程度上反對理學家的象數神秘主義。李冶曾批評朱熹著作,說它不通的地方很多。他指出,說數學難認識是可以的,但說數學不能認識就不對;他認為數學來源於自然界,“苟能推自然之理”就可以“明自然之數”。秦九韶雖曾主張數學與道學同出一源,但他後來也認識到,“通神明”的數學是不存在的,只有“經世務類萬物”的數學。
中西融合
明清時期
中國從明代開始進入了封建社會的晚期,16世紀末以後,西方初等數學陸續傳入中國,使中國數學研究出現一個中西融合貫通的局面;鴉片戰爭以後,近代數學開始傳入中國,中國數學便轉入一個以學習西方數學為主的時期;到19世紀末20世紀初,近代數學研究才真正開始。
從明初到明中葉,商品經濟有所發展,和這種商業發展相適應的是珠算的普及。明初《魁本對相四言雜字》和《魯班木經》的出現,說明珠算已十分流行。前者是兒童看圖識字的課本,後者把算盤作為家庭必需用品列入一般的木器家具手冊中。
發展衰落
這一時期指十四世紀中葉明王朝建立到明末的1582年。數學除珠算外出現全面衰弱的局面,當中涉及到中算的局限、十三世紀的考試制度中已刪減數學內容、明代大興八段考試制度等複雜的問題,不少中外數學史家仍探討當中涉及的原因。
明代最大的成就是珠算的普及,出現了許多珠算讀本,及至程大位的《直指算法統宗》〔1592〕問世,珠算理論已成系統,標誌著從籌算到珠算轉變的完成。但由於珠算流行,籌算幾乎絕跡,建立在籌算基礎上的古代數學也逐漸失傳,數學出現長期停滯。
珠算
1582年,義大利傳教士利瑪竇到中國,1607年以後,他先後與徐光啟翻譯了《幾何原本》前六卷、《測量法義》一卷,與李之藻編譯《圜容較義》和《同文算指》。1629年,徐光啟被禮部任命督修曆法,在他主持下,編譯《崇禎曆書》137卷。《崇禎曆書》主要是介紹歐洲天文學家第谷的地心學說。作為這一學說的數學基礎,希臘的幾何學,歐洲玉山若干的三角學,以及納皮爾算籌、伽利略比例規等計算工具也同時介紹進來。
在傳入的數學中,影響最大的是《幾何原本》。《幾何原本》是中國第一部數學翻譯著作,絕大部分數學名詞都是首創,其中許多至今仍在沿用。徐光啟認為對它“不必疑”、“不必改”,“舉世無一人不當學”。滿清侵入中原之後,科學再度被打入了“冷宮”。不但書的後半部分遲遲不能翻譯,就連徐光啟已經譯出的上半部分也不再發行。西方傳教士帶來的科技著作,成為康熙、雍正或乾隆皇帝獨享的業餘愛好。
其次套用最廣的是三角學,介紹西方三角學的著作有《大測》《割圓八線表》和《測量全義》。《大測》主要說明三角八線(正弦、餘弦、正切、餘切、正割、餘割、正矢、余矢)的性質,造表方法和用表方法。《測量全義》除增加一些《大測》所缺的平面三角外,比較重要的是積化和差公式和球面三角。所有這些,在當時曆法工作中都是隨譯隨用的。 中國數學史
中國數學史
 中國數學史
中國數學史1646年,波蘭傳教士穆尼閣來華,跟隨他學習西方科學的有薛鳳柞、方中通等。穆尼閣去世後,薛鳳柞據其所學,編成《歷學會通》,想把中法西法融會貫通起來。《歷學會通》中的數學內容主要有比例對數表》《比例四線新表》和《三角算法》。前兩書是介紹英國數學家納皮爾和布里格斯發明增修的對數。後一書除《崇禎曆書》介紹的球面三角外,尚有半角公式、半弧公式、德氏比例式、納氏比例式等。方中通所著《數度衍》對對數理論進行解釋。對數的傳入是十分重要,它在曆法計算中立即就得到套用。
清初學者研究中西數學有心得而著書傳世的很多,影響較大的有王錫闡《圖解》、梅文鼎《梅氏叢書輯要》(其中數學著作13種共40卷)、年希堯《視學》等。梅文鼎是集中西數學之大成者。他對傳統數學中的線性方程組解法、勾股形解法和高次冪求正根方法等方面進行整理和研究,年希堯的《視學》是中國第一部介紹西方透視學的著作。
清康熙重視西方科學,但只是作為自己的愛好。1712年康熙命梅彀成任蒙養齋彙編官,會同陳厚耀、何國宗、明安圖、楊道聲等編纂天文算法書。1721年完成《律歷淵源》100卷,以康熙“御定”的名義於1723年出版。其中《數理精蘊》主要由梅彀成負責,分上下兩編,上編包括《幾何原本》、《算法原本》,均譯自法文著作;下編包括算術、代數、平面幾何平面三角、立體幾何等初等數學,附有素數表、對數表和三角函式表。由於它是一部比較全面的初等數學百科全書,並有康熙“御定”的名義,因此對當時數學研究有一定影響。
清代數學家對西方數學做了大量的會通工作,並取得許多獨創性的成果。這些成果,如和傳統數學比較,是有進步的,但和同時代的西方比較則明顯落後了。
雍正即位以後,對外閉關自守,導致西方科學停止輸入中國,對內實行高壓政策,致使一般學者既不能接觸西方數學,又不敢過問經世致用之學,因而埋頭於究治古籍。乾嘉年間逐漸形成一個以考據學為主的乾嘉學派。
與傳統數學研究出現高潮的同時,阮元與李銳等編寫了一部天文數學家傳記—《疇人傳》,收集了從黃帝時期到嘉慶四年已故的天文學家和數學家270餘人(其中有數學著作傳世的不足50人),和明末以來介紹西方天文數學的傳教士41人。
1840年鴉片戰爭以後,西方近代數學開始傳入中國。首先是英人在上海設立墨海書館,介紹西方數學。第二次鴉片戰爭後,曾國藩、李鴻章等官僚集團開展“洋務運動”,也主張介紹和學習西方數學,組織翻譯了一批近代數學著作。
其中較重要的有李善蘭與偉烈亞力翻譯的《代數學》《代微積拾級》;華蘅芳與英人傅蘭雅合譯的《代數術》《微積溯源》《決疑數學》;鄒立文與狄考文編譯的《形學備旨》《代數備旨》《筆算數學》;謝洪賚與潘慎文合譯的《代形合參》《八線備旨》等等。
《代微積拾級》是中國第一部微積分學譯本;《代數學》是英國數學家德·摩根所著的符號代數學譯本;《決疑數學》是第一部機率論譯本。在這些譯著中,創造了許多數學名詞和術語,至今還在套用,但所用數學符號一般已被淘汰了。戊戌變法以後,各地興辦新法學校,上述一些著作便成為主要教科書。
在翻譯西方數學著作的同時,中國學者也進行一些研究,寫出一些著作,較重要的有李善蘭的《尖錐變法解》《考數根法》;夏彎翔的《洞方術圖解》《致曲術》《致曲圖解》等等,都是會通中西學術思想的研究成果。
由於輸入的近代數學需要一個消化吸收的過程,加上清末統治者十分腐敗,在太平天國運動的衝擊下,在列強的掠奪下,焦頭爛額,無暇顧及數學研究。直到1919年五四運動以後,中國近代數學的研究才真正開始。
整理研究
雍正即位(1723)以後,對外閉關自守,導致西方科學停止輸入中國,對內對漢族士大夫實行高壓政策。1773年開設四庫全書館,輯錄《永樂大典》保存佚書和徵集私家藏書,於1781年編成《四庫全書》,先後收集到《算經十書》和宋元時期的數學著作。纂修兼分校官戴震(1724~1777)對《周髀算經》、《九章算術》、《孫子算經》、《五經算術》 4部著作詳加校勘,改正許多誤文奪字,對學者是有幫助的。隨後,李潢(?~1811)著的《九章算術細草圖說》9卷,《海島算經細草圖說》1卷和《輯古算經考注》2卷,李銳注的《數書九章》、《測圓海鏡》和《益古演段》,沈欽裴著的《四元玉鑒細草》2 卷(1829)和羅士琳撰的《四元玉鑒細草》24卷(1834)都很有參考價值。
焦循在《加減乘除釋》(1798)中,用甲、乙、丙、丁……等天干字表示具體的數,列出加、減、乘、除的幾個基本定律,用這些符號和定律來說明古代算法原理,這在中國數學史上是一個創造。汪萊著有《衡齋算學》 7冊(1796~1805)。在第五冊(1801)中,他討論了二次、三次方程有多少正根以及正根和係數的關係問題,得到與韋達定理相當的結果。在第七冊(1805)中專門討論三項方程xn-pxm+q=0(n>m 都是正整數,p、q都是正數),他用歸納法得到上述方程有正根的條件相當於
1802年李銳見到汪萊的《衡齋算學》第五冊算書後,寫了“第五冊算書跋”,提出n次高次方程只有一個正根與多於一個正根和方程係數的符號有關,和得到一個正根後的(n-1)次方程的係數符號有關,他的結論基本上是正確的。在《開方說》(1817)中李銳進一步指出:高次方程係數符號變化一次的有1正根,變化二次的有2正根,變化三次的有3正根或1正根,變化四次的有4正根或2正根,所缺正根稱為“無數”,“凡無數必兩,無一無數者”。這些與笛卡兒的符號規則基本相同。他還指出:二次方程有2根,三次方程有3根或1根,四次方程有4根或2根(以上均包括負根);若方程有正、負根,將方程係數的正負號隔位易之,則正負根互換符號;方程的重根與“無數”不同等等。汪萊、李銳的工作,和宋元時代的代數學比較是青出於藍而勝於藍的;和西方代數學比較,在時間上晚了一些,但他們的成果是在沒有受到西方近代數學的影響下獨立得到的。 公式
公式
 公式
公式對朱世傑的垛積術進行研究並有重大成果的是李善蘭,在《垛積比類》(約1859)中,李善蘭創造了一個著名的恆等式:
利用三角垛求和公式就得出一個中外馳名的三角自乘垛求和公式: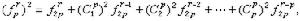 公式
公式
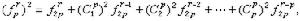 公式
公式與傳統數學研究出現高潮的同時,阮元與李銳等編寫了一部天文數學家傳記──《疇人傳》(1795~1810)。《疇人傳》收集從黃帝時期到嘉慶四年(1799)已故的天文學家和數學家270餘人(其中有數學著作傳世的不足50人)和明末以來介紹西方天文數學的傳教士 41人。這部著作全由“掇拾史書,荃萃群籍,甄而錄之”而成,收集的完全是第一手的原始資料,在學術界頗有影響。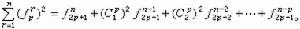 公式
公式
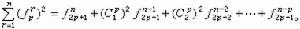 公式
公式傳統數學
乾嘉年間形成一個以考據學為主的乾嘉學派,編成《四庫全書》,其中數學著作有《算經十書》和宋元時期的著作,為保存瀕於湮沒的數學典籍做出重要貢獻。
在研究傳統數學時,許多數學家還有發明創造,例如有“談天三友”之稱的焦循、汪萊及李銳作出不少重要的工作。李善蘭在《垛積比類》〔約1859〕中得到三角自乘垛求和公式,稱之為“李善蘭恆等式”。這些工作較宋元時期的數學進了一步。阮元、李銳等人編寫了一部天文學家和數學家傳記《疇人傳》46卷〔1795-1810〕,開數學史研究之先河。
相關信息
高次方程
把增乘開方法推廣到數字高次方程(包括係數為負的情形)解法的是劉益(12世紀中期)。《楊輝算法》中《田畝比類乘除捷法》卷下介紹了原書中22個二次方程和1個四次方程,後者是用增乘開方法解三次以上的高次方程的最早例子。秦九韶是高次方程解法的集大成者,他在《數書九章》中收集了21個用增乘開方法解高次方程(最高次數為10)的問題。為了適應增乘開方法的計算程式,秦九韶把常數項規定為負數。他把高次方程解法分成各種類型,如:n次項係數不等於1的方程,奇次冪係數均為零的方程,進行x=y+с代換後常數項變號的方程與常數項符號不變而絕對值增大的方程等。方程的根為非整數時,秦九韶採取繼續求根的小數,或用減根變換方程各次冪的係數之和為分母、常數為分子來表示根的非整數部分,這是《九章算術》和劉徽注處理無理數方法的發展。在求根的第 2位數時,秦九韶還提出以一次項係數除常數項為根的第 2位數的試除法。秦九韶的方法比霍納方法早500多年。
從天元術推廣到二元、三元和四元的高次聯立方程組,是宋元數學家的又一項傑出的創造。祖頤在《四元玉鑒》後序中提到,平陽李德載《兩儀群英集臻》有天、地二元,霍山劉大鑒《乾坤括囊》有天、地、人三元。燕山朱漢卿“按天、地、人、物立成四元”。前二書已失傳,留傳至今並對這一傑出創造進行系統論述的是朱世傑的《四元玉鑒》。朱世傑的四元高次聯立方程組表示法無疑是在天元術的基礎上發展起來的,他把常數放在中央。四元的各次冪放在上、下、左、右四個方向上,其他各項放在四個象限中。朱世傑的最大貢獻是提出四元消元法。其方法是先擇一元為未知數,其他元組成的多項式作為這未知數的係數,列成若干個一元高次方程式,然後套用互乘相消法逐步消去這一未知數。重複這一步驟便可消去其他未知數,得到一個一元高次方程。最後用增乘開方法求解。這是線性方法組解法的重大發展。朱世傑的方法比西方同類方法早400多年。
內插法
一次同餘式組解法 《孫子算經》“物不知數”題已提到一次同餘式組解法的例子,秦九韶把它一般化。在這個方法中有一個必須解決的關鍵問題是求同餘式kiGi呏1(modαi)中的ki,式中秦九韶在《數書九章》大衍類里,用更相減損的方法給出ki一個計算程式,完滿地解決了這個問題,此外,秦九韶還討論了模數αi是收數(小數)、通數(分數)、元數(一般正整數)、複數(10n的倍數)非兩兩互素的情形,並分別給出變上述4種數為兩兩互素的模數的方法。高次方程立法用天元(相當於 x)作為未知數符號,立出高次方程,古代稱為天元術。這是中國數學史上首次引入符號,並用符號運算來解決建立高次方程的問題。現存最早的天元術著作是李冶的《測圓海鏡》。李冶在一次項係數右旁記一“元”字(或在常數項右旁記一“太”字)。元以上的係數分別表示各正次冪,元以下的係數表示常數和各負次冪(在《益古演段》中又把這個次序倒轉過來)。建立方程的具體方法是,根據問題的已知條件,列出兩個相等的多項式p1(x)和p2(x),令二者相減,即得一個數字高次方程。若其中一個多項式是分式多項式,如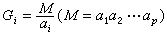 公式
公式
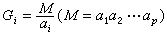 公式
公式,李冶則變另一多項式p2(x)為 公式
公式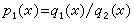 公式
公式
 公式
公式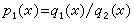 公式
公式這是劉徽關於率的概念在多項式運算中的套用與發展。 公式
公式
 公式
公式勾股解法
勾股形解法在宋元時期有新的發展,朱世傑在《算學啟蒙》卷下提出已知勾弦和、股弦和求解勾股形的方法,補充了《九章算術》的不足。李冶在《測圓海鏡》對勾股容圓問題進行了詳細的研究,得到一系列的結果。他把容圓勾股形分成14個相似的勾股形,除按傳統的方法給出這些勾股形的名稱外,還用文字作符號來表示,與現今用字母A,B,C,…表示幾何圖形相似。從14個勾股形中,李冶得到692條“識別雜記”,闡明各勾股形的線段之間與線段的和、差、積之間的關係。除原有的勾股容圓外,李冶得到勾上容圓、股上容圓、弦上容圓、勾股上容圓、勾外容圓、股外容圓、弦外容圓、勾外容圓半、股外容圓半等9個容圓公式,大大豐富了中國古代幾何學的內容。
弧矢割圓術
已知黃道與赤道的夾角和太陽從冬至點向春分點運行的黃經余弧,求赤經余弧和赤緯度數,是一個解球面直角三角形的問題。傳統曆法都是用內插法進行計算。元代王恂、郭守敬等則用傳統的勾股形解法、沈括的會圓術(已知弦、矢、半徑求弧長的近似公式)和天元術解決了這個問題。由於王恂、郭守敬求直徑時用圓周率3以及沈括的公式是一個近似公式,因此結果不夠精確。除此以外,整個推算步驟是正確無誤的。從數學意義上講,這個方法開闢了通往球面三角法的途徑。
縱橫圖
縱橫圖又稱幻方,根據《乾鑿度》和東漢鄭玄注,至遲在漢代已有一個三行縱橫圖。宋元時期,縱橫圖研究有了很大發展,楊輝在《續古摘奇算法》中記錄了這方面的成就。楊輝指出,九宮圖是一個從1~32的9個自然數排成三行三列,其行、列或對角線之和均為15的三行縱橫圖。這種圖可以推廣到從 1到n2的情形,它的行、列或對角線之和為n(1+n2)/2。他還列出四行、五行、六行、七行、八行、九行、十行8個縱橫圖,並指出三行和四行縱橫圖的構造方法。楊輝的這一工作為這個領域的研究開闢了道路。小數 現傳本《夏侯陽算經》已有化名數為十進小數的例子。宋元時代,這種十進小數有了廣泛套用和發展,秦九韶用名數作為小數的符號,例如18.56寸表示如圖1;李冶則依靠算式的位置表示,例如-8.25x2+2.673=0表示如圖2。楊輝和朱世傑的化斤價為兩價的歌訣,是小數的具體套用。
戰國時期的百家爭鳴也促進了數學的發展,一些學派還總結和概括出與數學有關的許多抽象概念。著名的有《墨經》中關於某些幾何名詞的定義和命題,例如:“圓,一中同長也”、“平,同高也”等等。墨家還給出有窮和無窮的定義。《莊子》記載了惠施等人的名家學說和桓團、公孫龍等辯者提出的論題,強調抽象的數學思想,例如“至大無外謂之大一,至小無內謂之小一”、“一尺之棰,日取其半,萬世不竭”等。這些許多幾何概念的定義、極限思想和其它數學命題是相當可貴的數學思想,但這種重視抽象性和邏輯嚴密性的新思想未能得到很好的繼承和發展。
此外,講述陰陽八卦,預言吉凶的《易經》已有了組合數學的萌芽,並反映出二進制的思想。
中國數學特點
⑴以算法為中心,屬於套用數學。中國數學不脫離社會生活與生產的實際,以解決實際問題為目標,數學研究是圍繞建立算法與提高計算技術而展開的。
⑵具有較強的社會性。中國傳統數學文化中,數學被儒學家培養人的道德與技能的基本知識---六藝(禮、樂、射、御、書、數)之一,它的作用在於“通神明、順性命,經世務、類萬物”,所以中國傳統數學總是被打上中國哲學與古代學術思想的烙印,往往與術數交織在一起。同時,數學教育與研究往往被封建政府所控制,唐宋時代的數學教育與科舉制度、歷代數學家往往是政府的天文官員,這些事例充分反映了這一性質。
⑶寓理於算,理論高度概括。由於中國傳統數學注重解決實際問題,而且因中國人綜合、歸納思維的決定,所以中國傳統數學不關心數學理論的形式化,但這並不意味中國傳統僅停留在經驗層次而無理論建樹。其實中國數學的算法中蘊涵著建立這些算法的理論基礎,中國數學家習慣把數學概念與方法建立在少數幾個不證自明、形象直觀的數學原理之上,如代數中的“率”的理論,平面幾何中的“出入相補”原理,立體幾何中的“陽馬術”、曲面體理論中的“截面原理”(或稱劉祖原理,即卡瓦列利原理)等等。
10、中國數學對世界的影響
數學活動有兩項基本工作----證明與計算,前者是由於接受了公理化(演繹化)數學文化傳統,後者是由於接受了機械化(算法化)數學文化傳統。在世界數學文化傳統中,以歐幾里得《幾何原本》為代表的希臘數學,無疑是西方演繹數學傳統的基礎,而以《九章算術》為代表的中國數學無疑是東方算法化數學傳統的基礎,它們東西輝映,共同促進了世界數學文化的發展。
中國數學通過絲綢之路傳播到印度、阿拉伯地區,後來經阿拉伯人傳入西方。而且在漢字文化圈內,一直影響著日本、朝鮮半島、越南等亞洲國家的數學發展。
其他相關信息
西方數學
十六世紀末開始,西方傳教士開始到中國活動,由於明清王朝制定天文曆法的需要,傳教士開始將與天文歷算有關的西方初等數學知識傳入中國,中國數學家在“西學中源”思想支配下,數學研究出現了一個中西融合貫通的局面。
十六世紀末,西方傳教士和中國學者合譯了許多西方數學專著。其中第一部且有重大影響的是義大利傳教士利馬竇和徐光啟合譯的《幾何原本》前6卷〔1607〕,其嚴謹的邏輯體系和演譯方法深受徐光啟推崇。徐光啟本人撰寫的《測量異同》和《勾股義》便套用了《幾何原本》的邏輯推理方法論證中國的勾股測望術。此外,《幾何原本》課本中絕大部份的名詞都是首創,且沿用至今。在輸入的西方數學中僅次於幾何的是三角學。在此之前,三角學只有零星的知識,而此後獲得迅速發展。介紹西方三角學的著作有鄧玉函編譯的《大測》〔2卷,1631〕、《割圓八線表》〔6卷〕和羅雅谷的《測量全義》〔10卷,1631〕。在徐光啟主持編譯的《崇禎曆書》〔137卷,1629-1633〕中,介紹了有關圓錐曲線的數學知識。
入清以後,會通中西數學的傑出代表是梅文鼎,他堅信中國傳統數學“必有精理”,對古代名著做了深入的研究,同時又能正確對待西方數學,使之在中國紮根,對清代中期數學研究的高潮是有積極影響的。與他同時代的數學家還有王錫闡和年希堯等人。清康熙帝愛好科學研究,他“御定”的《數理精蘊》〔53卷,1723〕,是一部比較全面的初等數學書,對當時的數學研究有一定影響。
1840年鴉片戰爭後,閉關鎖國政策被迫中止。同文館內添設“算學”,上海江南製造局內添設翻譯館,由此開始第二次翻譯引進的高潮。主要譯者和著作有:李善蘭與英國傳教士偉烈亞力合譯的《幾何原本》後9卷〔1857〕,使中國有了完整的《幾何原本》中譯本;《代數學》13卷〔1859〕;《代微積拾級》18卷〔1859〕。李善蘭與英國傳教士艾約瑟合譯《圓錐曲線說》3卷,華蘅芳與英國傳教士傅蘭雅合譯《代數術》25卷〔1872〕,《微積溯源》8卷〔1874〕,《決疑數學》10卷〔1880〕等。在這些譯著中,創造了許多數學名詞和術語,至今仍在套用。1898年建立京師大學堂,同文館併入。1905年廢除科舉,建立西方式學校教育,使用的課本也與西方其它各國相仿。
現代數學
這一時期是從20世紀初至今的一段時間,常以1949年新中國成立為標誌劃分為兩個階段。
中國近現代數學開始於清末民初的留學活動。較早出國學習數學的有1903年留日的馮祖荀,1908年留美的鄭之蕃,1910年留美的胡明復和趙元任,1911年留美的姜立夫,1912年留法的何魯,1913年留日的陳建功和留比利時的熊慶來〔1915年轉留法〕,1919年留日的蘇步青等人。他們中的多數回國後成為著名數學家和數學教育家,為中國近現代數學發展做出重要貢獻。其中胡明復1917年取得美國哈佛大學博士學位,成為第一位獲得博士學位的中國數學家。隨著留學人員的回國,各地大學的數學教育有了起色。最初只有北京大學1912年成立時建立的數學系,1920年姜立夫在天津南開大學創建數學系,1921年和1926年熊慶來分別在東南大學〔今南京大學〕和清華大學建立數學系,不久武漢大學、齊魯大學、浙江大學、中山大學陸續設立了數學系,到1932年各地已有32所大學設立了數學系或數理系。1930年熊慶來在清華大學首創數學研究部,開始招收研究生,陳省身、吳大任成為國內最早的數學研究生。三十年代出國學習數學的還有江澤涵〔1927〕、陳省身〔1934〕、華羅庚〔1936〕、許寶騤〔1936〕等人,他們都成為中國現代數學發展的骨幹力量。同時外國數學家也有來華講學的,例如英國的羅素〔1920〕,美國的伯克霍夫〔1934〕、奧斯古德〔1934〕、維納〔1935〕,法國的阿達馬〔1936〕等人。1935年中國數學會成立大會在上海召開,共有33名代表出席。1936年〈中國數學會學報〉和《數學雜誌》相繼問世,這些標誌著中國現代數學研究的進一步發展。解放以前的數學研究集中在純數學領域,在國內外共發表論著600餘種。在分析學方面,陳建功的三角級數論,熊慶來的亞純函式與整函式論研究是代表作,另外還有泛函分析、變分法、微分方程與積分方程的成果;在數論與代數方面,華羅庚等人的解析數論、幾何數論和代數數論以及近世代數研究取得令世人矚目的成果;在幾何與拓撲學方面,蘇步青的微分幾何學,江澤涵的代數拓撲學,陳省身的纖維叢理論和示性類理論等研究做了開創性的工作:在機率論與數理統計方面,許寶騤在一元和多元分析方面得到許多基本定理及嚴密證明。此外,李儼和錢寶琮開創了中國數學史的研究,他們在古算史料的注釋整理和考證分析方面做了許多奠基性的工作,使中國的民族文化遺產重放光彩。
1949年11月即成立中國科學院。1951年3月《中國數學學報》復刊〔1952年改為《數學學報》〕,1951年10月《中國數學雜誌》復刊〔1953年改為《數學通報》〕。1951年8月中國數學會召開建國後第一次國代表大會,討論了數學發展方向和各類學校數學教學改革問題。
建國後的數學研究取得長足進步。50年代初期就出版了華羅庚的《堆疊素數論》〔1953〕、蘇步青的《射影曲線概論》〔1954〕、陳建功的《直角函式級數的和》〔1954〕和李儼的《中算史論叢》5集〔1954-1955〕等專著,到1966年,共發表各種數學論文約2萬餘篇。除了在數論、代數、幾何、拓撲、函式論、機率論與數理統計、數學史等學科繼續取得新成果外,還在微分方程、計算技術、運籌學、數理邏輯與數學基礎等分支有所突破,有許多論著達到世界先進水平,同時培養和成長起一大批優秀數學家。
60年代後期,中國的數學研究基本停止,教育癱瘓、人員喪失、對外交流中斷,後經多方努力狀況略有改變。1970年《數學學報》恢復出版,並創刊《數學的實踐與認識》。1973年陳景潤在《中國科學》上發表《大偶數表示為一個素數及一個不超過二個素數的乘積之和》的論文,在哥德巴赫猜想的研究中取得突出成就。此外中國數學家在函式論、馬爾可夫過程、機率套用、運籌學、優選法等方面也有一定創見。
1978年11月中國數學會召開第三次代表大會,標誌著中國數學的復甦。1978年恢復全國數學競賽,1985年中國開始參加國際數學奧林匹克數學競賽。1981年陳景潤等數學家獲國家自然科學獎勵。1983年國家首批授於18名中青年學者以博士學位,其中數學工作者占2/3。1986年中國第一次派代表參加國際數學家大會,加入國際數學聯合會,吳文俊應邀作了關於中國古代數學史的45分鐘演講。近十幾年來數學研究碩果纍纍,發表論文專著的數量成倍增長,質量不斷上升。1985年慶祝中國數學會成立50周年年會上,已確定中國數學發展的長遠目標。代表們立志要不懈地努力,爭取使中國在世界上早日成為新的數學大國。

