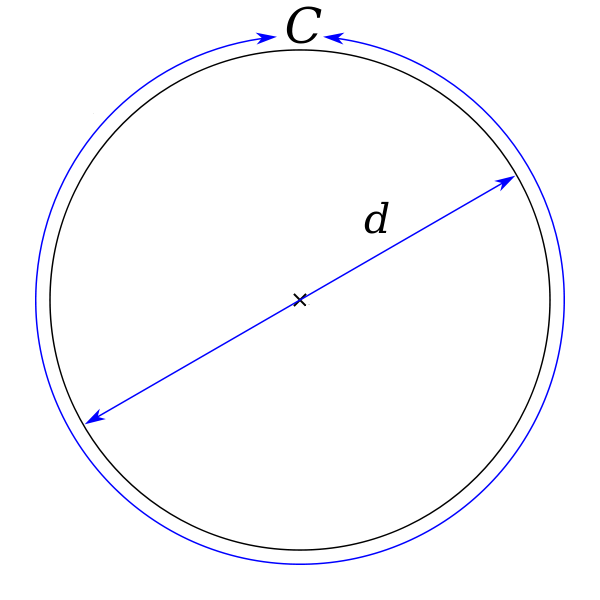
圓周率(Pi)是圓的周長與直徑的比值,一般用希臘字母π表示,是一個在數學及物理學中普遍存在的數學常數。π也等於圓形之面積與半徑平方之比。是精確計算圓周長、圓面積、球體積等幾何形狀的關鍵值。 在分析學里,π可以嚴格地定義為滿足sin x = 0的最小正實數x。
圓周率用希臘字母 π(讀作pài)表示,是一個常數(約等於3.141592654),是代表圓周長和直徑的比值。它是一個無理數,即無限不循環小數。在日常生活中,通常都用3.14代表圓周率去進行近似計算。而用十位小數3.141592654便足以應付一般計算。即使是工程師或物理學家要進行較精密的計算,充其量也只需取值至小數點後幾百個位。
1965年,英國數學家約翰·沃利斯(John Wallis)出版了一本數學專著,其中他推導出一個公式,發現圓周率等於無窮個分數相乘的積。2015年,羅切斯特大學的科學家們在氫原子能級的量子力學計算中發現了圓周率相同的公式。
2019年3月14日,谷歌宣布圓周率現已到小數點後31.4萬億位。
基本介紹
- 中文名:圓周率
- 外文名:Ratio of circumference to diameter;Pi
- 符號表示:π
- 近似值:22/7(約率)、355/113(密率)
歷史發展
實驗時期
幾何法時期




分析法時期

計算機時代
 圓周率
圓周率計算歷史
日期 | 計算者 | 國籍 | 正確位數 | 詳細紀錄 |
前20世紀 | 未知 | 1 | π= 3.125 | |
前20世紀 | 未知 | 1 | π= 3.160493... | |
前12世紀 | 未知 | 中國 | - | π=3 |
前6世紀中 | 聖經列王記上7章23節 | - | π=3 | |
前3世紀 | 3 | π=3.1418 | ||
公元前20年 | 1 | π= 3.125 | ||
公元前50年-公元前23年 | 中國 | 1 | π=3.1547 | |
130年 | 中國 | 1 | π=3.162277... | |
150年 | 未知 | 3 | π=3.141666... | |
250年 | 中國 | 1 | π=3.155555... | |
263年 | 中國 | 5 | π=3.14159 | |
480年 | 中國 | 7 | 3.1415926<π<3.1415927 | |
499年 | 印度 | 3 | π=3.1416 | |
598年 | 印度 | 1 | π=3.162277... | |
800年 | 烏茲別克 | 3 | π=3.1416 | |
印度 | 4 | π=3.14156 | ||
1220年 | 義大利 | 3 | π=3.141818 | |
1400年 | Madhava | 10 | π=3.14159265359 | |
1424年 | Jamshid Masud Al Kashi | π=16位小數 | ||
1573年 | Valentinus Otho | π=6位小數 | ||
1593年 | π=9位小數 | |||
1593年 | Adriaan van Roomen | π=15位小數 | ||
1596年 | π=20位小數 | |||
1615年 | π=32位小數 | |||
1621年 | 威理博·司乃耳, 范·科伊倫的學生 | π=35位小數 | ||
1665年 | π=16位小數 | |||
1699年 | Abraham Sharp | π=71位小數 | ||
1700年 | π=10位小數 | |||
1706年 | John Machin | π=100位小數 | ||
1706年 | William Jones | 引入希臘字母π | ||
1719年 | De Lagny | π=127位小數(只有112位正確) | ||
1723年 | π=41位小數 | |||
1730年 | Kamata | π=25位小數 | ||
1734年 | 引入希臘字母π並肯定其普及性 | |||
1739年 | 松永良弼 | π=50位小數 | ||
1761年 | 證明π是無理數 | |||
1775年 | 指出π可能是超越數 | |||
1794年 | Jurij Vega | π=140位小數(只有136位正確) | ||
1794年 | 阿德里安-馬里·勒讓德 | - | ||
1841年 | Rutherford | π=208位小數(只有152位正確) | ||
1844年 | Zacharias Dase及Strassnitzky | π=200位小數 | ||
1847年 | Thomas Clausen | π=248位小數 | ||
1853年 | Lehmann | π=261位小數 | ||
1853年 | William Rutherford | π=440位小數 | ||
1855年 | Richter | π=500位小數 | ||
1874年 | William Shanks | π=707位小數(只有527位正確) | ||
1882年 | Lindemann | 證明π是超越數 | ||
1946年 | D. F. Ferguson | π=620位小數 | ||
1947年 | π=710位小數 | |||
1947年 | π=808位小數 | |||
1949年 | J. W. Wrench爵士和L. R. Smith | π=2,037位小數(首次使用計算機) | ||
1955年 | J. W. Wrench爵士及L. R. Smith | π=3,089位小數 | ||
1957年 | G.E.Felton | π=7,480位小數 | ||
1958年 | Francois Genuys | π=10,000位小數 | ||
1958年 | G.E.Felton | π=10,020位小數 | ||
1959年 | Francois Genuys | π=16,167位小數 | ||
1961年 | IBM 7090電晶體計算機 | π=20,000位小數 | ||
1961年 | J. W. Wrench, Jr,及L. R. Smith | π=100,000位小數 | ||
1966年 | π=250,000位小數 | |||
1967年 | π=500,000位小數 | |||
1974年 | π=1,000,000位小數 | |||
1981年 | π=2,000,000位小數 | |||
1982年 | π=4,000,000位小數 | |||
1983年 | π=8,000,000位小數 | |||
1983年 | π=16,000,000位小數 | |||
1985年 | Bill Gosper | π=17,000,000位小數 | ||
1986年 | David H. Bailey | π=29,000,000位小數 | ||
1986年 | 金田康正 | π=33,000,000位小數 | ||
1986年 | π=67,000,000位小數 | |||
1987年 | π=134,000,000位小數 | |||
1988年 | π=201,000,000位小數 | |||
1989年 | 楚諾維斯基兄弟 | π=480,000,000位小數 | ||
1989年 | π=535,000,000位小數 | |||
1989年 | 金田康正 | π=536,000,000位小數 | ||
1989年 | 楚諾維斯基兄弟 | π=1,011,000,000位小數 | ||
1989年 | 金田康正 | π=1,073,000,000位小數 | ||
1992年 | π=2,180,000,000位小數 | |||
1994年 | 楚諾維斯基兄弟 | π=4,044,000,000位小數 | ||
1995年 | 金田康正和高橋大介 | π=4,294,960,000位小數 | ||
1995年 | π=6,000,000,000位小數 | |||
1996年 | 楚諾維斯基兄弟 | π=8,000,000,000位小數 | ||
1997年 | 金田康正和高橋大介 | π=51,500,000,000位小數 | ||
1999年 | π=68,700,000,000位小數 | |||
1999年 | π=206,000,000,000位小數 | |||
2002年 | 金田康正的隊伍 | π=1,241,100,000,000位小數 | ||
2009年 | 高橋大介 | π=2,576,980,370,000位小數 | ||
2009年 | π=2,699,999,990,000位小數 | |||
2010年 | 近藤茂 | π=5,000,000,000,000位小數 | ||
2011年 | π2的60,000,000,000,000位二進制小數 | |||
算準記錄
小數點後位數 | 首次算準者 | 首次算準時間 |
1 | 巴比倫人 | 前20世紀 |
2-3 | 前3世紀(距離上次1700年) | |
4-5 | 263年(距離上次563年以上) | |
6-7 | 480年(距離上次217年) | |
8-10 | Madhava | 1400年(距離上次920年) |
11-16 | Jamshid Masud Al Kashi | 1424年(距離上次24年) |
17-20 | 1596年(距離上次172年) | |
21-32 | 1615年(距離上次19年) | |
33-35 | 威理博·司乃耳, 范·科伊倫的學生 | 1621年(距離上次6年) |
36-71 | Abraham Sharp | 1699年(距離上次78年) |
72-100 | John Machin | 1706年(距離上次7年) |
101-112 | De Lagny | 1719年(距離上次13年) |
113-136 | Jurij Vega | 1794年(距離上次75年) |
137-152 | Rutherford | 1841年(距離上次47年) |
153-200 | Zacharias Dase及Strassnitzky | 1844年(距離上次3年) |
201-248 | Thomas Clausen | 1847年(距離上次3年) |
249-261 | Lehmann | 1853年(距離上次6年) |
262-440 | William Rutherford | 1853年(距離上次0年) |
441-500 | Richter | 1855年(距離上次2年) |
501-527 | William Shanks | 1874年(距離上次19年) |
528-620 | D. F. Ferguson | 1946年(距離上次72年) |
621-710 | 1947年(距離上次1年) | |
711-808 | 1947年(距離上次0年) | |
備註:這裡只列出人工計算的最高記錄,808位 | ||
記號





公式





















特性
幾何
| 平面圖形 | 周長 | 面積 |
|---|---|---|
圓 |  |  |
圓環 |  | |
扇形 |  |  |
註:①        ②周長、弧長用長度單位,面積用面積單位。 | ||
| 立體圖形 | 表面積 | 體積 |
|---|---|---|
圓柱 |  |  |
 | ||
 | ||
 | ||
圓錐 |  |  |
 | ||
註:①         ②底面周長用長度單位,表面積(含底面積和側面積)用面積單位,體積用體積單位或容積單位。 | ||
代數
數學分析

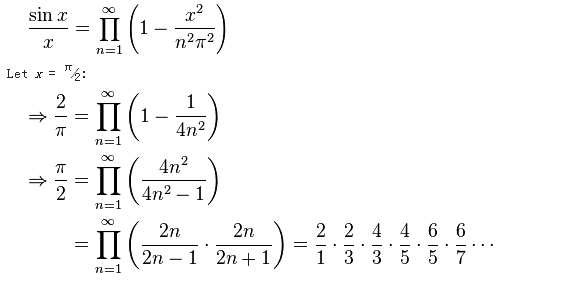
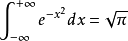

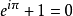


數論

機率論
統計學

物理學