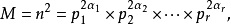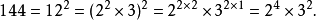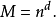質因子

質因子（或質因數）在數論里是指能整除給定正整數的質數。根據算術基本定理，不考慮排列順序的情況下，每個正整數都能夠以唯一的方式表示成它的質因數的乘積。兩個沒有共同質因子的正整數稱為互質。因為1沒有質因子，1與任何正整數（包括1本身）都是互質。只有一個質因子的正整數為質數。

基本介紹

• 中文名：質因子
• 外文名：prime factor
• 所屬學科：數學
• 定義：能整除給定正整數的質數
• 性質：兩個沒有共同質因子的正整數互質
• 相關定理：質因子分解式

定義

質因子（或質因數）在數論里是指能整除給定正整數的質數。根據算術基本定理，不考慮排列順序的情況下，每個正整數都能夠以唯一的方式表示成它的質因數的乘積。兩個沒有共同質因子的正整數稱為互質。因為1沒有質因子，1與任何正整數（包括1本身）都是互質。只有一個質因子的正整數為質數。

將一個正整數表示成質因數乘積的過程和得到的表示結果叫做質因數分解。顯示質因數分解結果時，如果其中某個質因數出現了不止一次，可以用冪次的形式表示。例如360的質因數分解是：

其中的質因數2、3、5在360的質因數分解中的冪次分別是3，2，1。

數論中的不少函式與正整數的質因子有關，比如取值為n的質因數個數的函式和取值為n的質因數之和的函式。它們都是加性函式，但並非完全加性函式。

例子

• 1沒有質因子。
• 5隻有1個質因子，5本身。（5是質數。）
• 6的質因子是2和3。(6 = 2×3)
• 2、4、8、16等只有1個質因子：2（2是質數，4 = 2²，8 = 2³，如此類推。）
• 100有2個質因子：2和5。(100 = 2²×5²)

完全平方數

完全平方數是指等於某個正整數的平方的數。比如225 = 15²是完全平方數，而226不是。完全平方數的質因數分解中，每個質因數的冪次都是偶數，這是因為假設完全平方數，則它的質因數分解可以從n的質因數分解推出。假設n的質因數分解是：

那么M的質因數分解就是：

所以每個質因子的冪次都是的形式，是偶數。

舉例來說，144是一個完全平方數：144 = 12²，它的質因數分解是：

類似地可以證明，如果某個正整數是完全立方數或某個正整數的冪次：，那么它的所有質因子的冪次都是d的倍數。

性質

• 兩個沒有共同質因子的正整數稱為互質。
• 數字1與任何正整數（包括1 本身）都是互質。
• 正整數的因數分解給出一連串的質因子；所有質因子相乘後。質因子如重複會以指數表示。
• 根據Fundamental theorem of arithmetic，任正整數有獨一無二的質因子分解式。
• 設任正整數n，其質因子數目及其質因子的和是n的算術函式(arithmetic function)。
• 例子 6的質因子是3和2。(6 = 3 × 2)
• 5隻有1個質因子，5本身。（5是質數。）
• 10有2個質因子：2和5。(10 = 2 x 5, 且10=5 x 2，只有2和5是質數)
• 2、4、8、16等只有1個質因子：2（2是質數，4 =2x 2，8 =2x 4，如此類推。偶數(6除外)的因子中，只有2是質數。）
• 1沒有質因子。（1是empty product）

互質關係

互質是兩個正整數之間的一種關係。如果兩個正整數a和b沒有共同的質因子，就稱這兩個正整數互質。一般來說兩個正整數的最大公約數是指能夠同時整除兩者的正整數之中最大的一個。如果a和b有公共的質因子p，那么它們的最大公約數gcd(a,b)就是p的倍數。a和b互質則說明最大公約數是1。

Ω函式

數論函式中與質因數有關的函式包括Ω函式和ω函式。ω函式定義為正整數n的不同質因子的個數，而Ω函式定義為計算每個質因數的冪次後正整數n的不同質因子的個數。

例如420的質因數分解是：

所以ω(420)=4，而Ω(420)= 2×1 + 1 + 1 + 1=5。因為420的質因數分解中2的冪次是2而其餘質因子的冪次是1。