短除法

簡介

短除法是求最大公因數的一種方法，也可用來求最低公倍數。求幾個數最大公因數的方法，開始時用觀察比較的方法，即：先把每個數的因數找出來，然後再找出公因數，最後在公因數中找出最大公因數。後來，使用分解質因數法來分別分解兩個數的因數，再進行運算。之後又演變為短除法。短除法運算方法是先用一個除數除以能被它除盡的一個質數，以此類推，除到商是質數為止。

基本方法

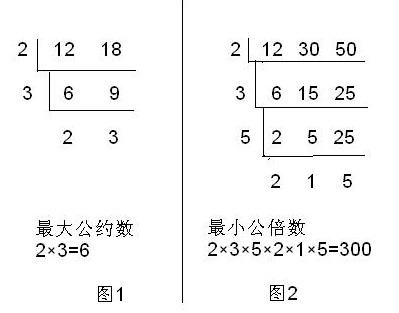公約數和公倍數

短除符號就是除號倒過來。短除就是在除法中寫除數的地方寫兩個數共有的質因數，然後落下兩個數被公有質因數整除的商，之後再除，以此類推，直到結果互質為止（兩個數互質）。

而在用短除計算公倍數數時，對其中任意兩個數存在的因數都要算出，其它沒有這個因數的數則原樣落下。直到剩下每兩個都是互質關係。

求最大公約數便乘一邊，求最低公倍數便乘一圈。

（公約數：亦稱“公因數”。是幾個整數同時均能整除的整數。如果一個整數同時是幾個整數的約數，稱這個整數為它們的“公約數”；公約數中最大的稱為最大公約數。）

基礎知識

如果數a能被數b整除，a就叫做b的倍數，b就叫做a的因數。因數和倍數都表示一個數與另一個數的關係，不能單獨存在。如只能說16是某數的倍數，2是某數的因數，而不能孤立地說16是倍數，2是因數。
"倍"與"倍數"是不同的兩個概念，"倍"是指兩個數相除的商，它可以是整數、小數或者分數。"倍數"只是在數的整除的範圍內，相對於"約數"而言的一個數字的概念，表示的是能被某一個自然數整除的數，它必須是一個自然數。
幾個自然數，公有的因數，叫做這幾個數的公因數；其中最大的一個，叫做這幾個數的最大公因數。例如：12、16的公約數有1、2、4，其中最大的一個是4，4是12與16的最大公約數，一般記為（12、16）=4。12、15、18的最大公約數是3，記為（12、15、18）=3。
幾個自然數公有的倍數，叫做這幾個數的公倍數，其中最小的一個，叫做這幾個數的最小的一個，叫做這幾個數的最低公倍數。例如：4的倍數有4、8、12、16，……，6的倍數有6、12、18、24，……，4和6的公倍數有12、24，……，其中最小的是12，一般記為[4、6]=12。12、15、18的最低公倍數是180。記為[12、15、18]=180。

分解質因數法

把每個數分別分解質因數，再把各數中的全部公有質因數提取出來連乘，所得的積就是
這幾個數的最大公約數。例如：求24和60的最大公約數，先分解質因數，得24=2×2×2×3，60=2×2×3×5，24與60的全部公有的質因數是2、2、3，它們的積是2×2×3=12，
所以，（24、60）=12。
把幾個數先分別分解質因數，再把各數中的全部公有的質因數和獨有的質因數提取出來連乘，所得的積就是這幾個數的最低公倍數。例如：求6和15的最低公倍數。先分解質因數，得6=2×3，15=3×5，6和15的全部公有的質因數是3，6獨有質因數是2，15獨有的質因數是5，2×3×5=30，30裡面包含6的全部質因數2和3，還包含了15的全部質因數3和5，且30是6和15的公倍數中最小的一個，所以[6，15]=30。

短除法

基本介紹

簡介

基本方法

基礎知識

分解質因數法

短除法

舉例說明

相關詞條

熱門詞條