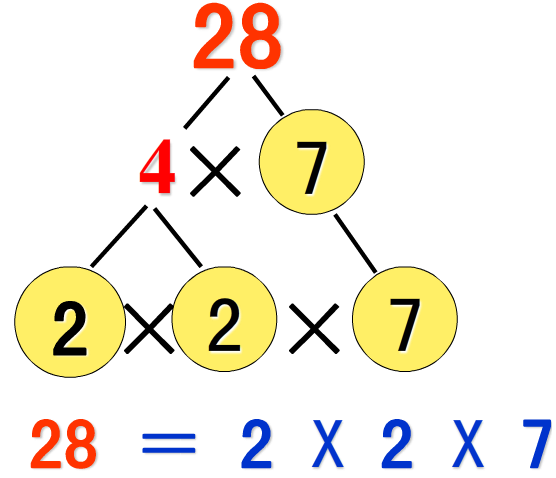
基本介紹
- 中文名：分解質因數
- 外文名：Prime factor decomposition
- 釋義：求質因數的過程
- 又稱：分解質因子
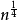
定義,定理,編程分解,
定義
把一個合數分解成若干個質因數的乘積的形式，即求質因數的過程叫做分解質因數。
定理
不存在最大質數的證明：（使用反證法）
假設存在最大的質數為N，則所有的質數序列為：N1，N2，N3……N
設M=（N1×N2×N3×N4×……N）+1，
可以證明M不能被任何質數整除，得出M也是一個質數。
第二種因數分解的方法：
1975年，John M. Pollard提出。該算法時間複雜度為O(
)。詳見參考資料。
編程分解
C#
static void Main(string[] args) { Practice3(); } private static void Practice3() { List<int> a = new List<int>(); //用於存放質因數 Console.WriteLine("請輸入一個整數："); int n = Convert.ToInt32(Console.ReadLine()); int o = n; //用於存放輸入的整數 for (int x = 2; x <= n; x++) { if(n%x == 0) { n/=x; a.Add(x); x--; //為了防止該整數有多個相同質因數最終只能輸出一個的情況 } } Console.WriteLine("{0}={1}",o,string.Join("*",a.ToArray())); }另一種實現
#include <stdio.h>Integer m,b,c := 0,j := 0;Integer a[10]; //存放質因數Integer fjzys(Integer k)beginInteger i := 2;while (k> := i) do //判斷k是否合格beginif (k mod i=0) then //判斷k是否整除當前因數begina[j] := i; //存入因數k/ := i; //餘數i := 2; //令i重新等於2j++; //計數值endelsebegini++; //不能整除則當前因數為非質因數end;end;(* C2PAS: Exit *) Result := 0;end;(* 用for實現上面的函式int fjzys(int k){int i=2;for ( ; i<=k ; i++ ) //當因數i<=k時，實現該循環，每次循環因數i自加1for ( ; k%i==0 ; j++ ) //當k整除當前因數，實現該循環，每次循環下標j自加1{k/=i; //使k=k/ia[j]=i; //存入因數}return 0;}解決上面的函式，無法輸出，多個相同的質因數，如90=2*3*3*5，只能輸出一個3.*)void main()beginprintf('請輸入一個整數'#10'k=');scanf('%d', (* C2PAS: RefOrBit? *)&m);fjzys(m);for(b := 0;b<(j-1);b++) //*比質因數少一個beginprintf('%d',a[b]);printf('*');end;printf('%d'#10'',a[j-1]); //輸出最後一個質因數end;pascal
//Pascal實現方法於2018.1.28更改，此前版本親測錯誤
//Pascal實現方法於2018.4.7再次更改，將可處理數字的範圍擴大了
{注意，此程式在處理過大的數字時速度不佳，在各大OJ上估計都會TLE幾個測試數據}Var n : Int64 ; i : Longint ;Begin readln( n ) ; if n<>1 then write( n , '=' ) else write( n , '=1' ); i := 2 ; while n<>1 do Begin if ( n mod i )=0 then Begin n := n div i ; write( i ); if n<>1 then write( '*' ); i := 2 ; End else inc( i ) ; End; writeln;End.//By Cubeneo（和之前的Rh。是同一個人）Java
import java.util.Scanner;public class H6 { public static void main(String[] args) { System.out.println("輸入所求正整數:"); Scanner sc = new Scanner(System.in); Long n = sc.nextLong(); long m=n; int flag = 0; String[] str = new String[50]; for (long i = 2; i <= n; i++) { if (n % i == 0) { str[flag] = Long.toString(i); flag++; n = n / i; i--; } } if (flag < 2) System.out.println(m + "為質數"); else { System.out.print(m + "=" + str[0]); for (int k = 1; k < flag; k++) { System.out.print("*" + str[k]); } System.out.println("\n"+m+"共有"+flag+"個質因數."); } sc.close(); }}此方法最多可分解包含50個質數的合數. @author寒鴉LMCVisual Basic
Dimx,a,b,kAsString PrivateSubCommand1_Click()a=Val(Text1.Text)x=2Ifa<=1Ora>Int(a)ThenIfa=1ThenText2.Text="它既不是質數，也不是合數"ElseMsgBox"請您先輸入數據",vbOKOnly+vbInformation,"友情提示"EndIfElseDoWhilea/2=Int(a/2）Anda>=4Ifb=0ThenText2.Text=Text2.Text&"2"b=1ElseText2.Text=Text2.Text&"*2"EndIfa=a/2k=aLoopDoWhilea>1Forx=3ToSqr(a)Step2DoWhilea/x=Int(a/x)Anda>=x*xIfb=0ThenText2.Text=Text2.Text&xb=1ElseText2.Text=Text2.Text&"*"&xEndIfa=a/xLoopNextk=aa=1LoopIfb=1ThenText2.Text=Text2.Text&"*"&kvElseText2.Text="這是一個質數"EndIfEndIfEndSubPrivateSubCommand2_Click()Text1.Text=""Text2.Text=""EndSub
c語言
實現一，此代碼因為用了long long int，為C99標準，故不可在VC6.0上運行。
#include <stdio.h>#include <math.h>int main(){ int i,b; long long int in;/*採用64位整型，以便輸入更大的數*/ freopen("F://1.txt","r",stdin); freopen("F://2.txt","w",stdout); while(scanf("%lld",&in)!=EOF) { /*在F://1.txt中輸入x個數N（N>=2）以換行符或空格符隔開，當沒有輸入時循環會自動結束*/ b=0;/*用於標記是否是第一個質因數，第一個質因數在輸出時前面不需要加空格*/ for(i=2;in!=1;i++) { if(in%i==0) { in/=i; b?printf("%d",i):printf("%d",i),b=1; i--; /*i--和i++使得i的值不變，即能把N含有的所有的當前質因數除盡，例如：24會一直把2除盡再去除3*/ } printf("\n"); } } return 0; }實現二
可直接在VC6.0運行。
#include <stdio.h>int m,b,c=0,j=0;int a[10]; //存放質因數int fjzys(int k){ int i=2; while(k>=i) //判斷k是否合格 { if(k%i==0) //判斷k是否整除當前因數 { a[j]=i; //存入因數 k/=i; //餘數 i=2; //令i重新等於2 j++; //計數值 } else { i++; //不能整除則當前因數為非質因數 } } return 0;}/* 用for實現上面的函式int fjzys(int k){ int i=2; for ( ; i<=k ; i++ ) //當因數i<=k時，實現該循環，每次循環因數i自加1 for ( ; k%i==0 ; j++ ) //當k整除當前因數，實現該循環，每次循環下標j自加1 { k/=i; //使k=k/i a[j]=i; //存入因數 } return 0;}解決上面的函式，無法輸出，多個相同的質因數，如90=2*3*3*5，只能輸出一個3.*/int main(){ printf("請輸入一個整數\nk="); scanf("%d", &m); fjzys(m); for(b=0;b<(j-1);b++) //*比質因數少一個 { printf("%d",a[b]); printf("*"); } printf("%d\n",a[j-1]); //輸出最後一個質因數 return 0;}C++語言
//將一個數n分解為若干個從小到大排列的質數的積#include <iostream>using namespace std;int main(){ int n, n2; cin >> n; cout << n << "="; n2 = n; if（n<2）return 0; //小於2的數不合法，若n為質數則輸出它本身 for(int i = 2;i*i<=n2;i++) //根號n複雜度 { while(n2%i==0) { n2=n2/i; cout << i ; if(n2!=1)cout << "*"; } } if（n2！=1） cout << n2; //當n為質數 return 0;}Common Lisp
(defun is-prime-number (number)
(let ((num number))
(do ((index 2 （1+ index)))
((>= index num) t)
(if (= 0 (mod num index))
(return-from is-prime-number nil)))))
(defun decomposition-quality-factor (number)
(let ((num number) (prime-list (make-array 10 :fill-pointer 0 :adjustable t)))
(if (is-prime-number num)
(progn
(format t "~a~%" num)
(return-from decomposition-quality-factor nil)))
(do ((index 2 （1+ index)))
((>= index num) nil)
(if (is-prime-number index)
(push index prime-list)))
(dolist (value prime-list)
(let ((test-flag nil))
(do ()
(test-flag nil)
(if (= 0 (mod num value))
(progn
(format t "~a~%" value)
(setf num (/ num value))
(if (is-prime-number num)
(progn
(format t "~a~%" num)
(return-from decomposition-quality-factor nil))))
(setf test-flag t)))))))
(let ((num number))
(do ((index 2 （1+ index)))
((>= index num) t)
(if (= 0 (mod num index))
(return-from is-prime-number nil)))))
(defun decomposition-quality-factor (number)
(let ((num number) (prime-list (make-array 10 :fill-pointer 0 :adjustable t)))
(if (is-prime-number num)
(progn
(format t "~a~%" num)
(return-from decomposition-quality-factor nil)))
(do ((index 2 （1+ index)))
((>= index num) nil)
(if (is-prime-number index)
(push index prime-list)))
(dolist (value prime-list)
(let ((test-flag nil))
(do ()
(test-flag nil)
(if (= 0 (mod num value))
(progn
(format t "~a~%" value)
(setf num (/ num value))
(if (is-prime-number num)
(progn
(format t "~a~%" num)
(return-from decomposition-quality-factor nil))))
(setf test-flag t)))))))
Python2.x分解質因數
#!/usr/bin/python# -*- coding:utf-8 -*-num = int(raw_input("請輸入要分解的正整數："))temp = []while num!=1: for i in range(2,num+1): if num%i == 0: temp.append(i) num /= i breakprint tempPython3.x分解質因數
#MillerRabin素數判定,結合Pollard_rho遞歸分解,效率極高import randomfrom collections import Counterdef gcd(a, b): if a == 0: return b if a < 0: return gcd(-a, b) while b > 0: c = a % b a, b = b, c return a def mod_mul(a, b, n): result = 0 while b > 0: if (b & 1) > 0: result = (result + a) % n a = (a + a) % n b = (b >> 1) return result def mod_exp(a, b, n): result = 1 while b > 0: if (b & 1) > 0: result = mod_mul(result, a, n) a = mod_mul(a, a, n) b = (b >> 1) return result def MillerRabinPrimeCheck(n): if n in {2, 3, 5, 7, 11}: return True elif (n == 1 or n % 2 == 0 or n % 3 == 0 or n % 5 == 0 or n % 7 == 0 or n % 11 == 0): return False k, u = 0, n - 1 while not (u & 1) > 0: k += 1 u = (u >> 1) random.seed(0) s = 5 for i in range(s): x = random.randint(2, n - 1) if x % n == 0: continue x = mod_exp(x, u, n) pre = x for j in range(k): x = mod_mul(x, x, n) if (x == 1 and pre != 1 and pre != n - 1): return False pre = x if x != 1: return False return True def Pollard_rho(x, c): (i, k) = (1, 2) x0 = random.randint(0, x) y = x0 while 1: i += 1 x0 = (mod_mul(x0, x0, x) + c) % x d = gcd(y - x0, x) if d != 1 and d != x: return d if y == x0: return x if i == k: y = x0 k += kdef PrimeFactorsListGenerator(n): result = [] if n <= 1: return None if MillerRabinPrimeCheck(n): return [n] p = n while p >= n: p = Pollard_rho(p, random.randint(1, n - 1)) result.extend(PrimeFactorsListGenerator(p)) result.extend(PrimeFactorsListGenerator(n // p)) return resultdef PrimeFactorsListCleaner(n): return Counter(PrimeFactorsListGenerator(n)) PrimeFactorsListCleaner(1254000000)Bash Shell分解質因數腳本
#!/usr/bin/bash
read input
factor "$input"
批處理分解質因數腳本
@echo offcolor 1e:start cls title 分解質因數程式 set /p num=請輸入待分解的數 set num0=%num% if %num% EQU 1 cls&echo 1既不是素數也不是非素數，不能分解&pause >nul&goto start if %num% EQU 2 cls&echo 2是素數，不能分解&pause >nul&goto start if %num% EQU 3 cls&echo 3是素數，不能分解&pause >nul&goto start set numx=:loop_1 if %num% EQU 1 goto result set count=3 set /a mod=%num%%%2 echo %mod% if %mod% EQU 0 ( set numx=%numx%×2&& set /a num=num/2 && goto loop_1 ):loop_2 set /a mod=%num%%%%count% if %mod% EQU 0 ( set numx=%numx%×%count%&& set /a num=num/count ) if %num% EQU 1 goto result if %count% EQU %num% set numx=%numx%×%count%&&goto result cls set /a stop=%count%*%count% if %stop% GTR %num% set numx=%numx%×%num%&& goto result set /a count+=2 echo 正在計算...... echo %num0%=%numx:~2% set /a wc=stop*100/num echo 正在計算%num%的因數 echo 已完成計算%wc%%% if %mod% EQU 0 goto loop_1 goto loop_2:result cls set numx=%numx:~1% if %num0% EQU %numx% echo %num0%是素數，不能分解！&pause >nul&goto start echo %num0%=%numx% pause >nul goto start
function prime(maxValue){ var minPrime = 2; var primes = [minPrime]; for(var i=3;i<=maxValue;i++){ var isPrime = true; for(var p=0;p<primes.length;p++){ if(i % primes[p] == 0){ isPrime = false; break; } } if(isPrime){ primes.push(i); } } return primes;}function decomposition(v){ var results = []; var primes = prime(v); var tmp = v; for(var i=0;i<primes.length;i++){ if(tmp == primes[i]){ results.push(primes[i]); break; } while(tmp % primes[i]==0){ tmp /= primes[i]; results.push(primes[i]); } } if(results.length == 1){ results = []; results.push(1); results.push(v); } return results;}