基本介紹
- 中文名:楊輝三角
- 外文名:Pascal's Triangle
- 別稱:賈憲三角形、帕斯卡三角形
- 表達式:幾何
- 提出者:楊輝
- 提出時間:約1050年
- 套用學科:數學,計算機
- 適用領域範圍:數學,計算機
- 使用人群:中學生、大學生,編程專家、等等
- 發現者:楊輝
簡介

概述
- 每個數等於它上方兩數之和。
- 每行數字左右對稱,由1開始逐漸變大。
- 第n行的數字有n項。
- 第n行的m個數可表示為 C(n-1,m-1),即為從n-1個不同元素中取m-1個元素的組合數。
- 第n行的第m個數和第n-m+1個數相等 ,為組合數性質之一。
- 每個數字等於上一行的左右兩個數字之和。可用此性質寫出整個楊輝三角。即第n+1行的第i個數等於第n行的第i-1個數和第i個數之和,這也是組合數的性質之一。即 C(n+1,i)=C(n,i)+C(n,i-1)。
- (a+b)n的展開式中的各項係數依次對應楊輝三角的第(n+1)行中的每一項。
- 將第2n+1行第1個數,跟第2n+2行第3個數、第2n+3行第5個數……連成一線,這些數的和是第4n+1個斐波那契數;將第2n行第2個數(n>1),跟第2n-1行第4個數、第2n-2行第6個數……這些數之和是第4n-2個斐波那契數。
- 將第n行的各數值,分別乘以10的列數m-1次方,然後把這些數值相加的和等於11的n-1次方。例子:第11行數分別為1,10,45,120,210,252,210,120,45,10,1,則11^10 = 1*10^0+10*10^1+45*10^2+...+1*10^10 =25937424601
套用
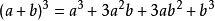
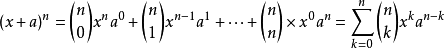
數在楊輝三角中的出現次數
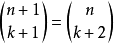
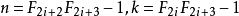
歷史沿革
- 賈憲 中國北宋 11世紀 《釋鎖算術》
- 楊輝 中國南宋1261《詳解九章算法》記載之功
- 阿爾·卡西 阿拉伯 1427《算術的鑰匙》
- 阿皮亞納斯 德國 1527
- 米歇爾.斯蒂費爾 德國 1544《綜合算術》二項式展開式係數
- 薛貝爾 法國 1545
- B·帕斯卡 法國 1654《論算術三角形》
在編程中實現
C++
#include<iostream>#include<iomanip>using namespace std;int main(){ const int n = 15; const int m = 2 * n-1; int arr[n + 1][m] = { 0 }; for (int i = 0; i < n; i++) { arr[i][n - i- 1] = 1; arr[i][n + i -1] = 1; } for (int i = 2; i < n; i++) { for (int j = n - i + 1; j < n-2+i; j = j + 2) arr[i][j] = arr[i - 1][j - 1] + arr[i - 1][j + 1]; } int p; for (int i = 0; i < n; i++) { for (int j = 0; j < n - i - 1; j++) cout << " "; p = 1; for (int j = n - i - 1; p < i + 2; j = j + 2) { cout << setw(4) << arr[i][j] << " "; p = p + 1; } cout << endl; } return 0;}Bash
#! /bin/bash# 用法:./pasTrig [個數],若不指明個數為 5。# 填充指定個數的空格pad(){ for ((k=0;k<$1;k++)); do echo -n ' '; done; }# 層數和新舊層lyrs=${1-5}prev[0]=1curr[0]=1 # 接下來每行第一個始終為一,無需重複賦值# 執行pad $(((lyrs-1)*2))echo 1for ((i=2; i<=lyrs; i++)); do # 略過 1,已處理 pad $(((lyrs-i)*2)) # 填充空格,注意這裡不會怎么顧及三位以上的數,即第 14 層開始會混亂 curr[i]=1 printf '%-4d' ${curr[0]} for ((j=1; j<i-1; j++)); do # 首尾極值已處理,略過 ((curr[j]=prev[j-1]+prev[j])) printf '%-4d' ${curr[j]} done printf '%-4d\n' ${curr[i]} # 最後一個和換行 # 搬家 prev=(${curr[*]}) done Bash 輸出楊輝三角並使用 nl 表明行號
Bash 輸出楊輝三角並使用 nl 表明行號C#
class Program{ public int yanghui(int value) { if(value<3) return 1; int[,]arry=new int[value,value]; Console.WriteLine("數組為:"); for(int i=0;i<value;i++) { string str=""; str=str.PadLeft(value-i); Console.Write(str); for(int j=0;j<=i;j++) { if(i==j||j==0) arry[i,j]=1; else arry[i,j]=arry[i-1,j-1]+arry[i-1,j]; Console.Write(arry[i,j]+""); } Console.WriteLine(); }} static void Main(string[]args){ Program p=new Program(); Console.WriteLine("請輸入數組值:"); if (p.yanghui(Convert.ToInt16(Console.ReadLine()))) Console.WriteLine("輸入數值必須大於3"); Console.Readkey();} }C
/* yh-rt1.c - 時間和空間最優算法 */#include <stdio.h>#include <stdlib.h>int main(){ int s = 1, h; // 數值和高度 int i, j; // 循環計數 scanf("%d", &h); // 輸入層數 printf("1\n"); // 輸出第一個 1 for (i = 2; i <= h; s = 1, i++) // 行數 i 從 2 到層高 { printf("1 "); // 第一個 1 for (j = 1; j <= i - 2; j++) // 列位置 j 繞過第一個直接開始循環 //printf("%d ", (s = (i - j) / j * s)); printf("%d ", (s = (i - j) * s / j)); printf("1\n"); // 最後一個 1,換行 } getchar(); // 暫停等待 return 0;} 默認狀態下不啟用金字塔和菱形的輸出
默認狀態下不啟用金字塔和菱形的輸出/* yh-2d.c - 二維數組疊代 */#include<stdio.h>#define M 10 // 行數// #define PYRAMID // 金字塔,會額外填充空格// #define REVERSE // 反向再來一次,得到菱形int main(void){ int a [M][M], i, j; // 二維數組和循環變數,a[行][列] for (i = 0; i<M; i++) // 每一行 {#ifdef PYRAMID for (j = 0;j <= M-i; j++) printf (" ");#endif // 填充結束 for (j = 0; j <= i; j++) // 賦值列印 printf("%4d", (a[i][j] = (i == j || j == 0) ? 1 : // 首尾置 1 a[i - 1][j] + a[i - 1][j - 1] )); // 使用上一行計算 printf("\n"); }#ifdef REVERSE for(i = M-2; i >= 0; i--) {#ifdef PYRAMID for (j = 0;j <= M - i; j++) printf(" ");#endif // 填充結束 for (j = 0;j <= i; j++) printf("%4d",a[i][j]); // 直接使用以前求得的值 printf("\n"); }#endif // 菱形結束 getchar(); // 暫停等待}/* yh-rt3.c - 較為暴力的大數組 */#include <stdio.h>#include "string.h"int main(){ int a[10000]; //容器,由n*(n+1)/2<=10000可知,n<=141 int b,CR,i; //b為當前行數,CR為要求顯示的行數,i為循環數 printf("請輸入要顯示的行數(3~141):"); scanf("%d",&CR); YHSJ(CR); a[1]=a[2]=1; //前兩行數值少且全為1,故直接輸出 printf("%d\n",a[1]); printf("%d %d\n",a[1],a[2]); for(b=3;b<=CR;b++) //從第三行開始判斷 { for(i=b;i>=2;i--) //從倒數第一個數開始加 a[i]=a[i]+a[i-1]; //楊輝三角的規律,沒有值的數組默認為0 for(i=1;i<=b;i++) //顯示循環 printf("%d ",a[i]); printf("\n"); // 換行 } return 0;}#include <stdio.h>#include <stdlib.h>#define EMPTY 1#define OFLOW 2#define INVAL 3#define MAX_Q 100typedef int DataType; // 數據類型選擇typedef struct{ DataType elem[MAX_Q]; int front, rear; } LinkQ;// 佇列及檢查宏#define InitQ(Q) LinkQ Q; Q.front=Q.rear=-1;#define _EQ(Q,e) Q.elem[(Q.rear=(Q.rear+1)%MAX_Q)]=e#define EnQ(Q,e) if((Q.rear+1)%MAX_Q==Q.front) Exit(OFLOW,"Overflow"); _EQ(Q,e)#define DeQ(Q,e) e=Q.elem[(Q.front=(Q.front+1)%MAX_Q)]#define Front(Q) Q.elem[(Q.front+1)%MAX_Q]// 退出int Exit(int err, char msg[]) { puts(msg); exit(err); return err; }int main(void){ int n=1,i,j,k,t; InitQ(Q); printf("please enter a number:"); scanf("%d",&n); if (n<=0) { printf("ERROR!\n"); exit(INVAL); } for(i=0;i<n;i++) printf(" "); puts("1"); EnQ(Q,1); EnQ(Q,1); for(i=1;i<n;i++) { for(k=0;k<n-i;k++) printf(" "); EnQ(Q,1); for(j=0;j<i;j++){ DeQ(Q,t); printf("%3d ",t); EnQ(Q,t+Front(Q)); } EnQ(Q,1); DeQ(Q,t); printf("%d\n",t); } return 0;}Visual Basic
Private Sub Form_Click() N = InputBox("", "", 5) ReDim a(N + 1, N + 1), b(N + 1, N + 1) Cls k = 8 For I = 1 To N Print String((N - I) * k / 2 + 1, " "); For J = 1 To I a(I, 1) = 1 a(I, I) = 1 a(I + 1, J + 1) = a(I, J) + a(I, J + 1) b(I, J) = Trim(Str(a(I, J))) Print b(I, J); String(k - Len(b(I, J)), " "); Next J Print Next IEnd SubSQL
-- 使用組合的計算公式和階乘計算楊輝三角,對大數容易溢出。create function Factorial (@count int) returns int as begin declare @ret int,@index int set @ret = 1 --初始值為 1 set @index = 1 while(@index <= @count) begin set @ret = @ret * @index set @index = @index + 1 end return (@ret)endcreate function Combination (@num int,@count int) returns int as begin declare @up int,@L1 int,@R1 int,@ret int set @up = dbo.Factorial(@count) set @L1 = dbo.Factorial(@num) set @R1 = dbo.Factorial(@count - @num) set @ret = @up/(@L1 * @R1) return (@ret)endcreate function PrintRow (@num int) returns nvarchar(100) as begin declare @i int declare @str nvarchar(100) set @str = '' set @i = 1 while (@i < @num) begin set @str = @str + replace(str(dbo.Combination(@i,@num)),' ','') + ' ,' set @i = @i + 1 end return (@str)endcreate proc PasTrigLines(@num int) as begin -- 主程式 declare @i int set @i = 1 while(@i <= @num ) begin if (@i = 0 ) print 1 + ',' else if (@i = 1) print '1,1,' else print '1,' + dbo.PrintRow(@i) + '1,' set @i = @i + 1 endendexec PasTrigLines 10 -- 十個
易語言
.版本 2.程式集 啟動視窗程式集 .程式集變數 帕斯卡三角階數, 整數型, , , 帕斯卡三角行數 .程式集變數 帕斯卡三角, 文本型, , , 形成的帕斯卡三角.子程式 __啟動視窗_創建完畢' 使用算法:遞歸調用 ' 問題:求帕斯卡(楊輝)三角 ' 問題描述:取N階的帕斯卡(楊輝)三角並顯示 ' 問題分析: ' 運用遞歸的方法取N層帕斯卡三角,並顯示。三角形邊界上的數都是1,內部的每個數是位於它上面的兩個數之和。 ' 假設f(row, col)表示楊輝三角的第row行的第col個元素,那么:f(row, col) = 1 (col = 1 或者 row = col),也就是遞歸的停止條件。f(row, col) = f(row - 1, col - 1) + f(row - 1, col),也就是上一行的兩個相鄰元素的和。遞歸調用求解。 ' 備註:.子程式 _計算圖形按鈕_被單擊 .局部變數 行數, 整數型, , , 帕斯卡三角行數 .局部變數 列數, 整數型, , , 帕斯卡三角列數 .局部變數 詢問返回, 整數型, , , 信息框返回的結果編輯框2.內容 = “” 帕斯卡三角 = “” ' 判斷輸入的值 .判斷開始 (編輯框1.內容 = “”) 信息框 (“輸入錯誤!”, 0, ) ' 當數值過大時,給出提示 .判斷 (到數值 (編輯框1.內容) > 20) 詢問返回 = 信息框 (“您輸入的數值過大,處理數據時程式將會有一段時間無回響,是否繼續?”, #是否鈕 + #詢問圖示, “請問:”) .如果真 (詢問返回 = #是鈕) ' 如果確定,調用求帕斯卡三角 求帕斯卡三角 () .如果真結束 ' 數據較小時調用求帕斯卡三角 .判斷 (編輯框1.內容 ≠ “” 且 到數值 (編輯框1.內容) ≤ 20) 求帕斯卡三角 () .默認.判斷結束 .子程式 求帕斯卡三角 .局部變數 行數, 整數型, , , 帕斯卡三角行數 .局部變數 列數, 整數型, , , 帕斯卡三角列數' 要求的帕斯卡三角的總行數 帕斯卡三角階數 = 到數值 (編輯框1.內容) - 1 .變數循環首 (0, 帕斯卡三角階數, 1, 行數) .變數循環首 (0, 行數, 1, 列數) ' 取帕斯卡三角元素放到當前行里 帕斯卡三角 = 帕斯卡三角 + 到文本 (取帕斯卡三角元素 (行數 + 1, 列數 + 1)) + “,” .變數循環尾 () 帕斯卡三角 = 取文本左邊 (帕斯卡三角, 取文本長度 (帕斯卡三角) - 1) + #換行符 ' 沒層需去尾都好加換行符 .變數循環尾 () ' 顯示結果 編輯框2.內容 = 帕斯卡三角 .子程式 取帕斯卡三角元素, 整數型, , 取帕斯卡三角中元素的子程式 .參數 行數, 整數型, , 帕斯卡三角行數 .參數 列數, 整數型, , 帕斯卡三角列數.如果 (列數 = 1 或 行數 = 列數) ' 每行的外圍兩個元素為1 返回 (1) .否則 ' 其餘的部分為上一行的(行數 - 1)和(行數)元素之和 返回 (取帕斯卡三角元素 (行數 - 1, 列數 - 1) + 取帕斯卡三角元素 (行數 - 1, 列數)) .如果結束
Java
public class TriangleArray{ public static void main(String[] args) { final int NMAX = 10; // allocate triangular array int[][] odds = new int[NMAX + 1][]; for (int n = 0; n <= NMAX; n++) odds[n] = new int[n + 1]; // fill triangular array for (int n = 0; n < odds.length; n++) for (int k = 0; k < odds[n].length; k++) { /* * compute binomial coefficient n*(n-1)*(n-2)*...*(n-k+1)/(1*2*3*...*k) */ int lotteryOdds = 1; for (int i = 1; i <= k; i++) lotteryOdds = lotteryOdds * (n - i + 1) / i; odds[n][k] = lotteryOdds; } // print triangular array for (int[] row : odds) { for (int odd : row) System.out.printf("%4d", odd); System.out.println(); } }}PHP
<?php/* 默認輸出十行,用T(值)的形式可改變輸出行數 */class T{ private $num; public function __construct($var=10) { if ($var<3) die("值太小啦!"); $this->num=$var; } public function display(){ $n=$this->num; $arr=array(); //$arr=array_fill(0,$n+1,array_fill(0,$n+1,0)); $arr[1]=array_fill(0,3,0); $arr[1][1]=1; echo str_pad(" ",$n*12," "); printf("%3d",$arr[1][1]); echo "<br/>"; for($i=2;$i<=$n;$i++){ $arr[$i]=array_fill(0,($i+2),0); for($j=1;$j<=$i;$j++){ if($j==1) echo str_pad(" ",($n+1-$i)*12," "); printf("%3d",$arr[$i][$j]=$arr[$i-1][$j-1]+$arr[$i-1][$j]); echo " "; } echo"<br/>"; } }}$yh=new T(); //$yh=new T(數量);$yh->display();?><?php$max = 10;$L = [1];var_dump($L);$L = [1,1];var_dump($L);$n = 2;while ($n <= $max - 1){ $oldL = $L; $L[$n] = 1; $n++; for ($i = 1;$i <count($oldL);$i++){ $L[$i] = $oldL[$i-1] + $oldL[$i]; } var_dump($L);}?>Python
# -*- coding: utf-8 -*-#!/usr/bin/env pythondef triangles(): L = [1] while True: yield L L = [sum(i) for i in zip([0]+L, L+[0])]
def triangles(): ret = [1] while True: yield ret for i in range(1, len(ret)): ret[i] = pre[i] + pre[i - 1] ret.append(1) pre = ret[:]
def YangHui (num = 10): LL = [[1]] for i in range(1,num): LL.append([(0 if j== 0 else LL[i-1][j-1])+ (0 if j ==len(LL[i-1]) else LL[i-1][j]) for j in range(i+1)]) return LL

