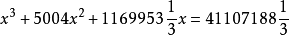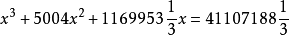基本介紹
- 書名：緝古算經
- 作者： 王孝通
- 成書地點：唐代長安
- 類型：數學
- 地區：中國
生平,成就,內容,歷史,試題,內容,第一問,第二問,第三問,第四問,第五問,第六問,第七問,第九問,第十問,第十一問,第十二問,第十三問,第十四問,第十五問,第十六問,第十七問,第十八問,第十九問,第二十問,版本,
生平
唐代立於學官的十部算經中，王孝通《緝古算經》是唯一的一部由唐代學者撰寫的。王孝通主要活動於六世紀末和七世紀初。他出身於平民，少年時期便開始潛心鑽研數學，隋朝時以歷算入仕，入唐後被留用，唐朝初年做過算學博士（亦稱算曆博士），後升任通直郎、太史丞。畢生從事數學和天文工作。
唐武德六年（623），因行用的傅仁均《戊寅元歷》推算日月食與實際天象不合，與吏部郎中祖孝孫受命研究傅仁均歷存在的問題，武德九年（626）又與大理卿崔善為奉詔校勘傅仁均歷，駁正術錯三十餘處，並付太史施行。
成就
內容
第一題為推求月球赤緯度數，屬於天文曆法方面的計算問題，第二題至十四題是修造觀象台、修築堤壩、開挖溝渠，以及建造倉廩和地窖等土木工程和水利工程的施工計算問題，第十五至二十題是勾股問題。這些問題反映了當時開鑿運河、修築長城和大規模城市建設等土木和水利工程施工計算的實際需要。
王孝通在《上緝古算經表》中說："伏尋《九章》商功篇有平地役功受袤之術。至於上寬下狹，前高后卑，正經之內闕而不論。致使今代之人不達深理，就平正之間同欹邪之用。斯乃圓孔方枘，如何可安。臣晝思夜想，臨書浩嘆，恐一旦瞑目，將來莫睹。遂於平地之餘，續狹邪之法，凡二十術，名曰《緝古》這段話清楚地說明了他寫作本書的目的和研究成果。
《緝古算經》涉及到立體體積計算、勾股計算、建立和求解三次方程x3+ax2+bx=A（a、b和A，非負），建立和求解雙二次方程x4+ax2=A（a、A，為正，這是一種特殊形式的四次方程）等數學內容。這類問題與解法大多相當複雜，就當時數學水平而言是相當困難的，因此，在國子監算學館要學習三年，學習年限僅次於祖氏父子的《綴術》。
例如該書第三題，假如從甲、乙、丙、丁四縣征派民工修築河堤，這段河堤的橫截面是等腰梯形，已知兩端上下底之差，兩端高度差，一端上底與高度差，一端高度與堤長之差，且已知各縣出工人數，每人每日平均取土量、隔山渡水取土距離、負重運輸效率和築堤土方量，以及完工時間等，求每人每日可完成的土方量，整段河堤的土方量（即河堤體積）和這段河堤的長度、兩端高度、兩端上下底寬度，以及各縣完成的堤段長度等。前兩個問題是比較簡單的算術問題，後兩個問題則要經過較複雜的推導和幾何變換歸結為建立和求解形如x3+ax2+bx=A的三次方程。
在《緝古算經》第十五題至二十題等屬於勾股算術的問題中，王孝通還創造性地把勾股問題引向三次方程，並與代數方法結合起來，擴大了勾股算術的範圍，發展了勾股問題的解題方法。
歷史
在中國數學史上，《緝古算經》是中國現存最早介紹開帶從立方法的算書，它集中體現了中國古代數學家早在公元七世紀在建立和求解三次方程等方面所取得的重要成就。在西方，雖然很早就已知道三次方程，但最初解三次方程是利用圓錐曲線的圖解法，一直到十三世紀義大利數學家菲波那契才有了三次方程的數值解法，這比王孝通晚了六百多年。王孝通對自己的研究成果十分得意。他在《上緝古算經表》中批評時人稱之精妙的《綴術》曾不覺方邑進行之術全錯不通，芻甍方亭之問於理未盡"，由於《綴術》已經失傳，王孝通的說法是否正確，已無從查考，但想來恐有失偏頗。他還宣稱，"請訪能算之人考論得失，如有排其一字，臣欲謝以千金"，這又未免有些過於自信。以後，宋元數學家創立了天元術、四元術和高次方程數值解法等，取得了更加輝煌的成就
試題
假今天正十一月朔夜半，日在斗十度七百分度之四百八十。以章歲為母，朔月行定分九千，朔日定小餘一萬，日法二萬，章歲七百，亦名行分法。今不取加時日度。問：天正朔夜半之時月在何處？（推朔夜半月度，舊術要須加時日度。自古先儒雖復修撰改制，意見甚眾，並未得算妙，有理不盡，考校尤難。臣每日夜思量，常以此理屈滯，恐後代無人知者。今奉敕造歷，因即改制，為此新術。舊推日度之術，巳得朔夜半日度，仍須更求加時日度，然知月處。臣今作新術，但得朔夜半日度，不須加時日度，即知月處。此新術比於舊術，一年之中十二倍省功，使學者易知）
答曰：在斗四度七百分度之五百三十。
內容
《緝古算經》全書共二十問，書首為《上緝古算術表》。各問題的形式大致相同，每問以“假令”開頭，以“問：……各幾何？”或“問：……個多少？”結尾；隨後是答案：“答曰……”；最後一段是“術曰”，詳細敘述建立方程的理論依據和具體程式。每題都有答案，但關於解題方法，王孝通則言簡意賅。
第一問
“假今天正十一月朔夜半，日在斗十度七百分度之四百八十。以章歲為母，朔月行定分九千，朔日定小餘一萬，日法二萬，章歲七百，亦名行分法。今不取加時日度。問：天正朔夜半之時月在何處？”。這是一道天文題，求半夜時月亮的赤道經度，王孝通用算術解題。
第二問
假令太史造仰觀台，上廣袤少，下廣袤多。上下廣差二丈，上下袤差四丈，上廣袤差三丈，高多上廣一十一丈，甲縣差一千四百一十八人，乙縣差三千二百二十二人，夏程人功常積七十五尺，限五日役台畢。羨道從台南面起，上廣多下廣一丈二尺，少袤一百四尺，高多袤四丈。甲縣一十三鄉，乙縣四十三鄉，每鄉別均賦常積六千三百尺，限一日役羨道畢。二縣差到人共造仰觀台，二縣鄉人共造羨道，皆從先給甲縣，以次與乙縣。台自下基給高，道自初登給袤。問：台道廣、高、袤及縣別給高、廣、袤各幾何？”。
對於這個建造觀象台和台道的廣度、高度、深度的計算，王孝通列出三個
第三問
“假令築堤，西頭上、下廣差六丈八尺二寸，東頭上、下廣差六尺二寸。東頭高少於西頭高三丈一尺，上廣多東頭高四尺九寸，正袤多於東頭高四百七十六尺九寸。甲縣六千七百二十四人，乙縣一萬六千六百七十七人，丙縣一萬九千四百四十八人，丁縣一萬二千七百八十一人。四縣每人一日穿土九石九斗二升。每人一日築常積一十一尺四寸十三分寸之六。穿方一尺得土八斗。古人負土二斗四升八合，平道行一百九十二步，一日六十二到。今隔山渡水取土，其平道只有一十一步，山斜高三十步，水寬一十二步，上山三當四，下山六當五，水行一當二，平道踟躕十加一，載輸一十四步。減計一人作功為均積。四縣共造，一日役華。今從東頭與甲，其次與乙、丙、丁。問：給斜、正袤與高，及下廣，並每人一日自穿、運、築程功，及堤上、下高、廣各幾何？
第一個三次方程：
第二個三次方程：
王孝通求得其解：31
第四問
“假令築龍尾堤，其堤從頭高、上闊以次低狹至尾。上廣多，下廣少，堤頭上下廣差六尺，下廣少高一丈二尺，少袤四丈八尺。甲縣二千三百七十五人，乙縣二千三百七十八人，丙縣五千二百四十七人。各人程功常積一尺九寸八分，一日役畢，三縣共築。今從堤尾與甲縣，以次與乙、丙。問：龍尾堤從頭至尾高、袤、廣及各縣別給高、袤、廣各多少。”
；解之得 x=18尺；
- 解之得 x=33尺；
第五問
“假令穿河，袤一裏二百七十六步，下廣六步一尺二寸；北頭深一丈八尺六寸，上廣十二步二尺四寸；南頭深二百四十一尺八寸；上廣八十六步四尺八寸。運土於河西岸造漘，北頭高二百二十三尺二寸，南頭無高，下廣四百六尺七寸五厘，袤與河同。甲郡二萬二千三百二十人，乙郡六萬八千七十六人，丙郡五萬九千九百八十五人，丁郡三萬七千九百四十四人。自穿、負、築，各人程功常積三尺七寸二分。限九十六日役，河漘俱了。四郡分共造漘，其河自北頭先給甲郡，以次與乙，合均賦積尺。問：逐郡各給斜、正袤，上廣及深，並漘上廣各多少？”
解二次方程，三次方程各一。
三次方程
： 得 方倉上底邊 x=3尺，下底邊=9尺，高=12尺。
第六問
“假令四郡輸粟，斛法二尺五寸，一人作功為均。自上給甲，以次與乙。其甲郡輸粟三萬八千七百四十五石六斗，乙郡輸粟三萬四千九百五石六斗，丙郡輸粟，二萬六千二百七十石四斗，丁郡輸粟一萬四千七十八石四斗。四郡共穿窖，上袤多於上廣一丈，少於下袤三丈，多於深六丈，少於下廣一丈。各計粟多少，均出丁夫。自穿、負、築，冬程人功常積一十二尺，一日役。問：窖上下廣、袤、深，郡別出人及窖深、廣各多少？”
解兩個三次方程。
第七問
“假令亭倉上小下大，上下方差六尺，高多上方九尺，容粟一百八十七石二斗。今已運出五十石四斗。問：倉上下方、高及余粟深、上方各多少？”
第八問
“假令芻甍上袤三丈，下袤九丈，廣六丈，高一十二丈。有甲縣六百三十二人，乙縣二百四十三人。夏程人功當積三十六尺，限八日役。自穿築，二縣共造。今甲縣先到。問：自下給高、廣、袤、各多少？”是關於建築觀象台、河堤、糧窖等工程中的土方問題。
解一個三次方程：
得 乙縣工程 高 x=72尺; 甲縣工程高=120-72=48尺、上廣=36尺 、袤=66尺。
第九問
“假令圓囤上小下大，斛法二尺五寸，以率徑一周三。上下周差一丈二尺，高多上周一丈八尺，容粟七百五斛六斗。今已運出二百六十六石四斗。問：殘粟去口、上下周、高各多少？”
解兩個三次方程。
第十問
“假令有粟二萬三千一百二十斛七斗三升，欲作方倉一，圓窖一，盛各滿中而粟適盡。令高、深等，使方面少於圓徑九寸，多於高二丈九尺八寸，率徑七，周二十二。問：方、徑、深多少？”
解一個三次方程。
第十一問
“假令有粟一萬六千三百四十八石八斗，欲作方倉四、圓窖三，令高、深等，方面少於圓徑一丈，多於高五尺，斛法二尺五寸，率徑七，周二十二。問：方、高、徑多少？”
解一個三次方程。
第十二問
“假令有粟三千七十二石，欲作方倉一、圓窖一，令徑與方等，方於窖深二尺，少於倉高三尺，盛各滿中而粟適盡（圓率、斛法並與前同）。問：方、徑、高、深各多少？”
解一個三次方程。
第十三問
“假令有粟五千一百四十石，欲作方窖、圓窖各一，令口小底大，方面於圓徑等，兩深亦同，其深少於下方七尺，多於上方一丈四尺，盛各滿中而粟適盡（圓率、斛法並與前同）。問：方、徑、深各多少？”
解一個三次方程。
第十四問
“假令有粟二萬六千三百四十二石四斗，欲作方窖六、圓窖四，令口小底大，方面與圓徑等，其深亦同，令深少於下方七尺，多於上方一丈四尺，盛各滿中而粟適盡（圓率、斛法並與前同）。問上下方、深數各多少？”
解一個三次方程。
第十五問
“假令有句股相乘冪七百六十五分之一，弦多於句三十六十分之九。問：三事各多少？”
解一個三次方程：
。
第十六問
“假令相乘冪四千七百三十九五分之三，句少於弦五十四五分之二。問：股多少？”
解一個三次方程。
第十七問
“假令有句弦相乘冪一千三百三十七二十分之一，弦多股一、十分之一。問：股多少？”
解一個三次方程。“答曰：九十二五分之二。”
“術曰：冪自乘，倍多而一，為立冪。又多再自乘，半之，減立冪，余為實。又多數自乘，倍之，為方法。又置多數，五之，二而一，為廉法，從。開立方除之，即股（句弦相乘冪自乘，即句冪乘弦冪之積。故以倍股弦差而一，得一股與半差為方，令多再自乘半之為隅，橫虛二立廉……倍之為從隅……多為上廣即二多……法故五之二而一）。”
王孝通所述，相當於建立一個三次方程：
第十八問
“假令有股弦相乘冪四千七百三十九五分之三，句少於弦五十四五分之二。問：股多少？”
解一個三次方程。
第十九問
“假令有股弦相乘冪七百二十六，句七、十分之七。問：股多少？”
解一個雙二次方程。
第二十問
“假令有股十六二分之一，句弦相乘冪一百六十四二十五分之十四。問：句多少？”
解一個雙二次方程：
