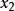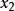基本介紹
筆算方法,方法一,方法二,歷史記載,九章算術,開立方原文,開根號原理,方法,原理,注意細節,
筆算方法
方法一
1．將被開立方數的整數部分從個位起向左每三位分為一組；
2．根據最左邊一組，求得立方根的最高位數；
3．用第一組數減去立方根最高位數的立方，在其右邊寫上第二組數；
4．用求得的最高位數的平方的300倍試除上述餘數，得出試商；並把求得的最高位數的平方的300倍與試商的積、求得的最高位數的30倍與試商的平方的積和試商的立方寫在豎式左邊，觀察其和是否大於餘數，若大於，就減小試商再試，若不大於，試商就是立方根的第二位數；
5．用同樣方法繼續進行下去。
方法二
第1、2步同上。
第三步，商完後，落下餘數和後面緊跟著的三位，如果後面沒有就把餘數後面添上三個0；
第四步，將要試商的數代入式子“已商數×要試商數×（10×已商數+要試商數）×30+要商數的立方”，最接近但不超過第三步得到的數者，即為這一位要商的數。
然後重複第3、4步，直到除盡。
歷史記載
九章算術
《九章算術》中講了開平方、開立方的方法，所不同的是古代用籌算進行演算，現以少廣章第12題為例，說明古代開平方演算的步驟，“今有積五萬五千二百二十五步，問為方幾。”答曰：“二百三十五步。”這裡所說的步是我國古代的長度單位。
開立方原文
開立方
〔立方適等，求其一面也。〕
術曰：置積為實。借一算，步之，超二等。
〔言千之面十，言百萬之面百。〕
議所得，以再乘所借一算為法，而除之。
〔再乘者，亦求為方冪。以上議命而除之，則立方等也。〕
除已，三之為定法。
〔為當復除，故豫張三面，以定方冪為定法也。〕
復除，折而下。
〔復除者，三面方冪以皆自乘之數，須得折、議，定其厚薄爾。開平冪者，
方百之面十；開立冪者，方千之面十。據定法已有成方之冪，故復除當以千為百，
折下一等也。〕
以三乘所得數，置中行。
〔設三廉之定長。〕
復借一算，置下行。
〔欲以為隅方。立方等未有定數，且置一算定其位。〕
步之，中超一，下超二等。
〔上方法，長自乘而一折，中廉法，但有長，故降一等；下隅法，無面長，
故又降一等也。〕
復置議，以一乘中，
〔為三廉備冪也。〕
再乘下，
〔令隅自乘，為方冪也。〕
皆副以加定法。以定法除。
〔三面、三廉、一隅皆已有冪，以上議命之而除，去三冪之厚也。〕
除已，倍下，並中，從定法。
〔凡再以中、三以下，加定法者，三廉各當以兩面之冪連於兩方之面，一隅
連於三廉之端，以待覆除也。言不盡意，解此要當以棋，乃得明耳。〕
復除，折下如前。開之不盡者，亦為不可開。
〔術亦有以定法命分者，不如故冪開方，以微數為分也。〕
開根號原理
方法
1、數m開n次方，n位一節為一根，前根均作a，a後需求的根均作b；前根a的位數不斷增長，後根b永遠作一位根視；直至開盡或開至所需要的位數。
原理
正向乘方式：m=（a+b），n=an+bn+s（s根據n的數字而定值）
逆向開方時：m－a^n=b^n+s=x^n+s；m－a^n－b^n=s；
如二次方的s=2ab；
三次方的s=3abD（D=a+b）；
五次方的s=5abD（D^2－ab）；
其它任意次方的固律參數照推。
即：b^n=m－a^n－s=c－s（c為可知數，s、b^n為潛態可知數）
例如：（a+b）^3=a^3+b^3+3(a^2)b+3a(b^2)=a^3+b^3+3ab（a+b）= m=a^3+b^3+3abD(D=a+b)
所以：（a+b）^3=m=a^3+b^3+3abD(D=a+b)
其他任意高次方的轉換方式理同最簡單、用式最短的三次方原理實用式記法。
但m開3次方時，這個原公式幫不上忙了，即必須進行轉換。
因此成：（a+b）^3=a^3+b^3+3(a^2)b+3a(b^2)=a^3+b^3+3ab（a+b）=m= a^3+b^3+3abD(D=a+b)，
而後面轉換成為m=a^3+b^3+3abD(D=a+b)，則m開方時就有同二次方一樣的公式[求根式]可用了，在任意高次方中理同二次方無異。
也即在實際開高次方或無窮大指數時，或高次方程的運算過程中（注意：求b=x根就是科學上的各種一元n次方的標準方程式），《結構數學》都將現代數學式中的式子按照“結構原理”進行了處理與轉換，使它都按照統一規律形式的規律型公式去表達，目的：便於快速簡潔的進行運算，並符合“算術公里的無矛盾性標準”。
注意細節
m=（a+b）^2=a^2+b^2+2ab=aa+bb+2ab；這個2ab就是二次方的S；所以二次方都會解！
而：
m=（a+b）^3=a^3+b^3+3(a^2)b+3a(b^2)=aaa+bbb+3aab+3abb=a^3+b^3+3ab（a+b）= a^3+b^3+3abD【D=a+b】；這個3abD就是三次方的S；
又如，m=（a+b）^5=a^5+b^5+5(a^4)b+10(a^3)(b^2)+10(a^2)(b^3)+5a(b^4)= a^5+b^5+5abD(D^2-ab)
五次方的S=5abD(D^2-ab) =5(a^4)b+10(a^3)(b^2)+10(a^2)(b^3)+5a(b^4)。
而這些3ab（a+b）=3abD=S；5abD(D^2-ab) =5(a^4)b+10(a^3)(b^2)+10(a^2)(b^3)+5a(b^4)=S，這個S就是高次方程解的奧秘。
在無窮大次方中，你知道了S，那么高次方的解同二次低方解的S=2ab的方式、方法沒有任何區別的簡單的不值一文錢了，也沒有任何解的障礙或稱為難題的必要了。
例如，A=5，k=3.
公式：5介於1^3至2^3之間（1的3次方=1，2的3次方=8）
第一步：
={2.0+[5/(2.0^2-2.0]1/3=1.7}。輸入值大於輸出值，負反饋；
即5/2×2=1.25，1.25-2=-0.75，0.75×1/3=0.25，
2-0.25=1.75，取2位數值，即1.7。
第二步：
={1.7+[5/(1.7^2-1.7]1/3=1.71}。輸入值小於輸出值，正反饋；
即5/1.7×1.7=1.73010，1.73-1.7=0.03，0.03×1/3=0.01，
1.7+0.01=1.71。取3位數，比前面多取一位數。
第三步：
={1.71+[5/(1.71^2-1.71]1/3=1.709}。輸入值大於輸出值，負反饋；
第四步：
={1.709+[5/(1.709^2-1.709]1/3=1.7099}.輸入值小於輸出值，正反饋；
這種方法可以自動調節，第一步與第三步取值偏大，但是計算出來以後輸出值會自動轉小；第二步，第四步輸入值偏小，輸出值自動轉大 =1.7099.
當然也可以取1.1，1.2，1.3，...，1.8，1.9中的任何一個。
開平方公式
例如，A=5：
5介於2的平方至3的平方之間。我們取初始值2.1，2.2，2.3，2.4，2.5，2.6，2.7，2.8，2.9都可以，我們最好取 中間值2.5。
第一步：2.5+（5/2.5-2.5)1/2=2.2；
即5/2.5=2，2-2.5=-0.5，-0.5×1/2=-0.25，2.5+(-0.25)=2.25，取2位數2.2。
第二步：2.2+(5/2.2-2.2)1/2=2.23；
即5/2.2=2.27272，2.27272-2.2=-0.07272，-0.07272×1/2=-0.03636，2.2+0.03636=2.23。取3位數2.23。
第三步：2.23+(5/2.23-2.23)1/2=2.236。
即5/2.23=2.2421525，
2.2421525-2.23=0.0121525，
0.0121525×1/2=0.00607，
2.23+0.006=2.236，取4位數。
每一步多取一位數。這個方法又叫反饋開方，即使你輸入一個錯誤的數值，也沒有關係，輸出值會自動調節，接近準確值。
