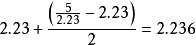初等代數中,二項式是只有兩項的多項式,即兩個單項式的和。
二項式是僅次於單項式的最簡單多項式。
基本介紹
- 中文名:二項式
- 外文名:binomial
- 地位:單項式外的最簡多項式
- 定義:只有兩項的多項式
- 意義:兩個單項式的和
- 適用範圍:數理科學
運算法則,與因子相乘,兩二項式相乘,二項式平方,二項式的冪,二項式因式分解,二項式的遞推,形式,線性形式,複數形式,定理,組合數,係數性質,賦值法,數形趣遇,
運算法則
與因子相乘
二項式與因子 c 的乘法可以根據分配律計算:

兩二項式相乘
兩個二項式a+b與c+d的乘法可以通過兩次分配律得到:

兩個線性二項式ax+b與 cx+d 的乘積為:

二項式平方
二項式a+b的平方為

二項式a-b的平方為

二項式的冪
二項式因式分解


二項式的遞推
二項式展開後各項的係數依次為:圖——推廣公式其中,第1個數=1,從第2個數開始,後面的每一個數都可以用前面的那個數表示為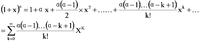 推廣公式
推廣公式
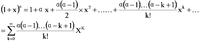 推廣公式
推廣公式這就是二項式展開“係數遞推”的依據. 二項式係數遞推實際上是組合數由到的遞推。
形式
線性形式
如果二項式的形式為ax+b(其中a與b是常數,x是變數),那么這個二項式是線性的。
複數形式
複數是形式為a+bi的二項式,其中i是-1的平方根。
定理
binomial theorem


其中,二項式係數指

等號右邊的多項式叫做二項展開式。
二項展開式的通項公式為

其i項係數可表示為n取i的組合數目。
組合數
1、

2、

3、

證明:由 可得
可得

當a=b=1時,代入二項式定理可證明1
當a=-1,b=1時代入二項式定理可證明2
4.組合數的性質:
(1)

(2)

(3)

係數性質
①對稱性
②增減性和最大值:先增後減
n為偶數時,中間一項的二項式係數最大,為

n為奇數時,中間兩項的二項式係數相等且最大,為 ,
,


賦值法
掌握“賦值法”這種利用恆等式解決問題的思想.
二項式係數之和:2n
而且展開式中奇數項二項式係數之和等於偶數項二項式係數之和等於

二項式定理的推廣:
二項式定理推廣到指數為非自然數的情況:
形式為 .
.

數形趣遇
二項式定理與楊輝三角形是一對天然的數形趣遇,它把數形結合帶進了計算數學. 求二項式展開式係數的問題,實際上是一種組合數的計算問題. 用係數通項公式來計算,稱為“式算”;用楊輝三角形來計算,稱作“圖算”.
1 4 6 4 1
1 5 10 10 5 1
…… 15 20 15 6 …
1 …… 35 35 21 ……
… 70 56 …
圖上得到=70,=56.
故求得展開式中常數項為70 – 2×56 = – 42
【點評】“式算”與“圖算”趣遇,各揚所長,各補所短.
楊輝三角形本來就是二項式展開式的算圖. 對楊輝三角形熟悉的考生,比如他熟悉到了它的第6行:
1,6,15,20,15,6,1
那么他可以心算不動筆,對本題做到一望而答.
利用二項式推出牛頓切線法開方
開立方公式:
設A = X^3,求X.稱為開立方。 開立方有一個標準的公式:

例如,A=5,,即求
5介於1的3次方;至2的3次方;之間(1的3次方=1,2的3次方=8)
初始值X0可以取1.1,1.2,1.3,1.4,1.5,1.6,1.7,1.8,1.9,都可以。例如我們取X0 = 1.9按照公式:
第一步: ,即
,即 ,
, ,
, ,
, 。即取2位數值,即1.7。
。即取2位數值,即1.7。





第二步: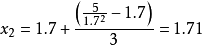 ,即
,即 ,
, ,
, ,
, 。取3位數,比前面多取一位數。
。取3位數,比前面多取一位數。
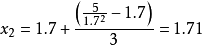




第三步: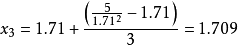
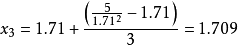
第四步:

這種方法可以自動調節,第一步與第三步取值偏大,但是計算出來以後輸出值會自動轉小;第二步,第四步輸入值偏小,輸出值自動轉大。即 ;當然初始值X0也可以取1.1,1.2,1.3,...1.8,1.9中的任何一個,都是X1 = 1.7 。當然,我們在實際中初始值採用中間值,即1.5。
;當然初始值X0也可以取1.1,1.2,1.3,...1.8,1.9中的任何一個,都是X1 = 1.7 。當然,我們在實際中初始值採用中間值,即1.5。

如果用這個公式開平方,只需將3改成2,2改成1。即

例如,A=5:
5介於2的平方至3的平方之間。我們取初始值2.1,2.2,2.3,2.4,2.5,2.6,2.7,2.8,2.9都可以,我們取中間值2.5。 第一步: ;
;

即 ,取2位數2.2。
,取2位數2.2。

第二步: ;
;

即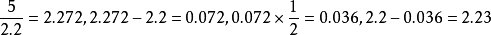 。取3位數。
。取3位數。