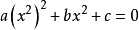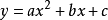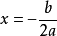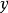雙二次方程

雙二次方程又稱“準二次方程”，是移項且合併同類項之後，只含有偶次項的四次方程；換句話講，形如ax^4+bx^2+c=0（其中a、b、c均為不等於零的複數）的一元四次方程叫做雙二次方程。實際上，通過變數替換y=x^2可以將雙二次方程轉化成關於y的一元二次方程：ay^2+by+c=0，先求解出 y 的值，在求出解 x 的值。需要注意的是，求出來的結果一定經過驗證，看是否是原方程的解。

基本介紹

• 中文名：雙二次方程
• 外文名：Double two equation
• 別名：準二次方程
• 定義：只含有偶次項的一元四次方程
• 領域：數學
• 求解注意事項：需要驗證

定義

雙二次方程又稱“準二次方程”，是移項且合併同類項之後，只含有偶次項的四次方程，其一般形式為：。

換句話說，形如（其中a、b、c均為不等於零的複數）的一元四次方程叫做雙二次方程。實際上，通過變數替換可以將雙二次方程轉化成關於y的一元二次方程：。

求方程的解

已知：（其中a、b、c均為不等於零的複數），求該方程的解。

無實數解情形

這個方程在複數集中有解。我們只討論無實數解的情況：

解這個方程一般方法是化為同解方程：，以一元二次方程的解法解得，再由此得到。由於要求找到無法滿足方程的實數的情形，因此可能有以下情形：

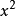（1）不是實數；

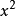
（2）解得的兩個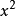均滿足

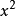
下面分情況討論：

（1）對應的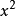關於的一元二次方程的；

（2）關於的一元二次方程有兩個負實根。此時（若（1）不成立則一定滿足這個條件），以原方程中作為自變數，對應的拋物線和軸的交點都在的負半軸上。於是對稱軸在軸左側，即；且代入時，。

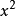
綜上所述：若滿足或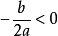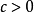（）的其中之一時，則原方程無實數解。

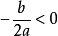
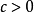
求解步驟

第一步，令可以將雙二次方程轉化成關於y的一元二次方程：

第二步，求解上述一元二次方程，得：

第三部，得到雙二次方程求根公式為：

第四部，驗證所求的解是否是原方程的根。

注意事項

求解雙二次方程一定要有驗根的步驟，看是否在實數的範圍內。

典型例題

例1

解方程。

解：令，可以將雙二次方程轉化成關於y的一元二次方程：；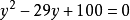

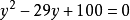
上式等價於：；

得：；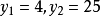

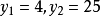
由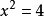，可以得到：；

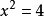
由，可以得到：；

經驗證，均為原方程的解。

例2

解方程。

解：令，可以將雙二次方程轉化成關於y的一元二次方程：；

上式等價於：；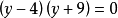

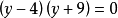
得：；

由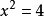，可以得到：；

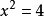
由，可知在實數範圍內無解，故捨去；

經驗證，為原方程的解。