簡介 19世紀末20世紀初形成的一個數學分支,它的最基本內容已成為分析數學各分支的普遍基礎。實變函式主要指
自變數 (也包括多變數)取實數值的函式,而實變函式論就是研究一般實變函式的理論。
在
微積分學 中,主要是從
連續 性、
可微 性、
黎曼可積 性三個方面來討論函式(包括函式序列的
極限函式 )。如果說微積分學所討論的函式都是性質“良好”的函式(例如往往假設函式連續或只有有限個
間斷點 ),那么,實變函式論是從連續性、可微性、可積性三個方面討論最一般的函式,包括從微積分學來看性質“不好”的函式。它所得到的有關的結論自然也適用於性質“良好”的函式。實變函式論是微積分學的發展和深入。
函式可積性的討論是實變函式論中最主要的內容。它包括
勒貝格 (Henri Léon Lebesgue) 的
測度 、
可測集 、可測函式和積分以及少許更一般的勒貝格-斯蒂爾傑斯測度 (Lebesgue-Stieltjes Measure)和積分的理論(見
勒貝格積分 )。這種積分比
黎曼積分 是更為普遍適用和更為有效的工具,例如
微積分基本定理 以及積分與
極限 變換次序。精美的
調和分析 理論(見
傅立葉分析 )就是建立在勒貝格積分的基礎上的。此外,還適應特殊的需要而討論一些特殊的積分。例如為討論牛頓-萊布尼茨公式而有佩隆積分(Perron integral)。由於有了具有可列可加性的測度和建立在這種測度基礎上的積分,導致了與微積分中函式序列的點點收斂和
一致收斂 不同的一些新的重要收斂概念的產生,它們是幾乎處處收斂、
度量 收斂(亦稱依測度收斂)、積分平均收斂等。度量收斂在
機率論 中就是依機率收斂,且具有特別重要的地位。積分平均收斂在一般分析學科中也是常用的重要收斂。
傅立葉級數 理論以及一般的
正交級數 理論就是以積分的平方平均收斂為基本的收斂概念。一般正交級數的無條件收斂問題在實變函式論中也有所討論。
在函式連續性方面,實變函式論考察了例如定義在直線的子集
(不必是
區間 )上的函式的不連續點的特徵:
第一類間斷點 最多只有可列個,
第二類間斷點 必是可列個(相對於
的)
閉集 的
並集 (也稱和集)的結論;還討論怎樣的函式可以表示成
連續函式 序列處處收斂的極限,引入半連續函式,更一般地是引入貝爾函式(Baire function),並討論它們的結構。
與研究函式連續性密切相關的就是討論各類重要的點集如
,更一般的是
波萊爾集 及其結構。解析集合論就是在深入討論波萊爾集和勒貝格可測集相互關係基礎上形成的一個數學分支。實變函式論在函式可微性方面所獲得的結果是非常深刻的。設
是定義在
上的、在每點取有限值的實函式。對於每個
,引入四個數:
分別稱
為
在
處的右方上(下)導數,左方上(下)導數(統稱為Dini derivative)。這四個數(可以是無限大)都相等且有限時,就稱
在
處是
可導 的。歷史上人們曾以為
上任何連續函式
都至少有一點是可導的,後來
維爾斯特拉斯 (Karl Weierstrass)舉出了一個反例:
,式中
,而
是奇數且
。
它是連續的,而在任何一點處都是不可導的。但按A·當儒瓦(Arnaud Denjoy) ,W·Н·楊 (William Young) 和S·薩克斯 (Stanisław Saks) 的工作結果,有Denjoy–Young–Saks theorem 如下:對
上每點取有限值的實函式,必有
勒貝格測度 是零的集
,使得對任何
,下面三種情況必有一種出現。①
在
處有有限導數。②在
處的異側的某兩個導數是同一個有限數;另兩個異側導數必定一個是
,另一個是
。③兩個上導數都是
,兩個下導數都是
。由這個定理又可推出如下重要結果:設
是
上單調函式,那么除去一個勒貝格測度是零的集外,必定存在且有限。
勒貝格.H.L 在實變函式論中還考慮可導點集的特徵,
多元函式 的微分問題以及其他的一些導數概念和不同導數之間的關係。實變函式論不僅套用廣泛,是某些數學分支的基本工具,而且它的觀念和方法以及它在各個數學分支的套用,對形成
近代數學 的
一般拓撲學 和
泛函分析 兩個重要分支有著極為重要的影響。
產生 實變函式論的產生
微積分產生於十七世紀,到了十八世紀末十九世紀初,微積分學已經基本上成熟了。數學家廣泛地研究並建立起它的許多分支,是它很快就形成了數學中的一大部門,也就是
數學分析 。
也正是在那個時候,數學家逐漸發現分析基礎本身還存在著很多問題。比如,什麼是函式這個看上去簡單而且十分重要的問題,數學界並沒有形成一致的見解。以至長期爭論者問題的這樣和那樣的解答,這樣和那樣的數學結果,弄不清究竟誰是正確的。又如,對於什麼是連續性和連續函式的性質是什麼,數學界也沒有足夠清晰的理解。
十九世紀初,曾經有人試圖證明任何連續函式除個別點外總是可微的。後來,德國數學家維爾斯特拉斯提出了一個由
級數 定義的函式,這個函式是連續函式,但是維爾斯特拉斯證明了這個函式在任何點上都不可導。這個發現使許多數學家大為吃驚。
由於發現了某些函式的奇特性質,數學家對函式的研究更加深入了。人們又陸續發現了有些函式是連續的但處處不可微,有的函式的有限導數並不黎曼可積;還發現了連續但是不分段單調的函式等等。這些都促使數學家考慮,人們要處理的函式,僅僅依靠直觀觀察和猜測是不行的,必須深入研究各種函式的性質。比如,連續函式必定可積,但是具有什麼性質的不連續函式也可積呢?如果改變積分的定義,可積分條件又是什麼樣的?連續函式不一定可導,那么可導的充分必要條件由是什麼樣的?……
上面這些函式性質問題的研究,逐漸產生了新的理論,並形成了一門新的學科,這就是實變函式。
內容 綜述 以實數作為自變數的函式就做實變函式,以實變函式作為研究對象的數學分支就叫做實變函式論。它是微積分學的進一步發展,它的基礎是點集論。什麼是點集論呢?點集論是專門研究點所成的集合的性質的理論。也可以說實變函式論是在點集論的基礎上研究分析數學中的一些最基本的概念和性質的。比如,點集函式、序列、極限、連續性、可微性、積分等。實變函式論還要研究實變函式的分類問題、結構問題。
實變函式論的內容包括實值函式的連續性質、微分理論、積分理論和
測度論 等。這裡我們只對它的一些重要的基本概念作簡要的介紹。
實變函式論的積分理論研究各種積分的推廣方法和它們的運算規則。由於積分歸根到底是數的運算,所以在進行積分的時候,必須給各種點集以一個數量的概念,這個概念叫做測度。
測度 什麼是測度呢?簡單地說,一條線段的長度就是它的測度。測度的概念對於實變函式論十分重要。集合的測度這個概念實由法國數學家勒貝格提出來的。
為了推廣積分概念,1893年,約當(Camille Jordan)在他所寫的《分析教程》中,提出了“約當容度”(Jordan measure)的概念並用來討論積分。1898年,法國數學家波萊爾(Borel, Emile)(把容度的概念作了改進,並把它叫做測度。波萊爾的學生勒貝格後來發表《積分、長度、面積》的論文,提出了“勒貝格測度”、“勒貝格積分”的概念。勒貝格還在他的論文《積分和圓函式的研究》中,證明了有界函式黎曼可積的充分必要條件是不連續點構成一個零測度集,這就完全解決了黎曼可積性的問題。
勒貝格積分可以推廣到無界函式的情形,這個時候所得積分是
絕對收斂 的,後來由推廣到積分可以不是絕對收斂的。從這些就可以看出,勒貝格積分比起由柯西給出後來又由黎曼發揚的老積分定義廣大多了。也可以看出,實變函式論所研究的是更為廣泛的函式類。
自從維爾斯特拉斯證明連續函式必定可以表示成一致收斂的多項式級數,人們就認清連續函式必定可以解析地表達出來,連續函式也必定可以用多項式來逼近。這樣,在實變函式論的領域裡又出現了
逼近論 的理論。
逼近理論 什麼是逼近理論呢?舉例來說,如果能把 A類函式表示成B類函式的極限,就說A類函式能以B類函式來逼近。如果已經掌握B類函式的某些性質,那么往往可以由此推出A類函式的相應性質。逼近論就是研究那一類函式可以用另一類函式來逼近、逼近的方法、逼近的程度和在逼近中出現的各種情況。
和逼近理論密切相關的有正交級數理論,三角級數就是一種正交級數。和逼近理論相關的還有一種理論,就是從某一類已知函式出發構造出新的函式類型的理論,這種理論叫做函式構造論。
運用 (L)測度這一工具,通過引入列導數(或導出數)的概念,在研究函式的可微性方面獲得了一系列深刻的結果,單調可微定理就是其中之一,意義在[a,b]上的單調函式在[a,b]E上處處可導,且導函式在[a,b]上是(L)可積的(這裡E表示[a,b]中(L)測度為零的子集),此外,也可利用(L)積分的理論和點集分析的方法討論多元實變函式的微分問題。在收斂性方面 ,實變函式論利用(L)測度和(L)積分工具,引入了幾乎處處收斂、依測度收斂(或度量收斂)和積分平均收斂等概念。依測度收斂就是機率論中的依機率收斂,在機率論中具有重要的地位,而積分平均收斂在分析數學中是刻劃收斂性態時常用的工具之一,傅立葉級數理論以及一般正交級數理論中就是以
均方 收斂為基本收斂概念的。實變函式論不僅在現代數學,尤其是分析數學中有著廣泛的套用,而且它的理論和方法對於形成近代數學的其他分支,例如拓撲學、泛函分析有直接的影響。
分支學科 








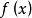
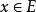








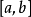
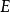
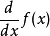
 勒貝格.H.L
勒貝格.H.L