基本介紹
- 中文名:約束最最佳化問題
- 外文名:constrained optimization problem
- 所屬學科:數學
- 所屬領域:運籌學(非線性規劃)
簡介

解法


















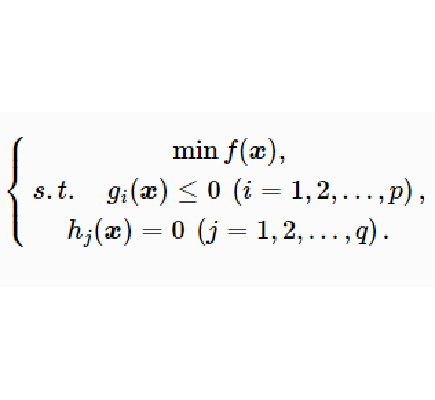



















約束最佳化問題(亦譯為受約束的最最佳化問題)是一類數學最最佳化問題,它由目標函式以及與目標函式中的變數相關的約束條件兩部分組成,最佳化過程則為在約束條件下最最佳化(最大化或最小化)目標函式。方程一般形式 一個約束最小化問題可以寫成...
工程設計中最最佳化問題(optimization problem)的一般提法是要選擇一組參數(變數),在滿足一系列有關的限制條件(約束)下,使設計指標(目標)達到最優值。因此,最最佳化問題通常可以表示為數學規劃形式的問題。概念 工程設計中最最佳化問題...
約束最佳化(Constrained Optimization),即約束最佳化問題,是最佳化問題的分支。它是在一系列約束條件下,尋找一組參數值,使某個或某一組函式的目標值達到最優。其中約束條件既可以是等式約束也可以是不等式約束。尋找這一組參數值的關鍵可是:...
約束最佳化法(Constrained Optimization Method):約束最佳化問題是在自變數滿足約束條件的情況下目標函式最小化的問題,其中約束條件既可以是等式約束也可以是不等式約束。將約束最佳化問題作為一個的研究方向主要起源於以下兩點:(1) 大多數實際...
約束最佳化方法是尋求具有約束條件的線性或非線性規劃問題解的數值算法。假設ƒ(尣),gi(尣)(i=1,2,…,m)是n維歐幾里得空間Rn中的實值函式。所謂約束最佳化問題,是指在約束條件gi(尣)≤0(i=1,2,…,m)之下求一點,使ƒ(尣)≥...
最最佳化方法,是指解決最最佳化問題的方法。所謂最最佳化問題,指在某些約束條件下,決定某些可選擇的變數應該取何值,使所選定的目標函式達到最優的問題。即運用最新科技手段和處理方法,使系統達到總體最優,從而為系統提出設計、施工、管理、...
《約束無導數最最佳化問題的理論與方法及其套用》是依託上海師範大學,由朱德通擔任項目負責人的面上項目。項目摘要 本項目將提供約束無導數最佳化問題的理論研究和方法及其數值分析。將技巧地使用線搜尋技術/信賴域策略,結合序貫二次規劃方法和...
有約束最最佳化 有約束最最佳化是有約束最小化和有約束最大化的統稱。參見“非線性規劃”。
最最佳化是套用數學的一個分支,主要指在一定條件限制下,選取某種研究方案使目標達到最優的一種方法。最最佳化問題在當今的軍事、工程、管理等領域有著極其廣泛的套用。發展歷史 隨著科學技術的日益發展,許多工程的核心問題最終都歸結為最佳化...
無約束最最佳化問題(unconstrained optimizationproblem)指的是從一個問題的所有可能的備選方案中,選擇出依某種指標來說是最優的解決方案。從數學上說,最最佳化是研究在一個給定的集合S上泛函J(u)的極小化或極大化問題:廣義上,最最佳化...
無約束最最佳化方法是求解無約束最最佳化問題的方法,有解析法和直接法兩類。簡介 無約束最最佳化方法是求解無約束最最佳化問題的方法,有解析法和直接法兩類。分類 解析法 解析法就是利用無約束最最佳化問題中目標函式 f(x) 的解析表達式和它...
《正交約束最佳化問題及其套用》是依託上海交通大學,由文再文擔任項目負責人的青年科學基金項目。項目摘要 變數是正交矩陣的最佳化問題出現在科學與工程中的很多重大套用中,如p-調和流理論,線性與非線性特徵值問題, 組合最佳化問題的鬆弛解,二...
無約束最最佳化 無約束最最佳化(unconstrained optimizations),指無約束最小化和無約束最大化的統稱。參見“非線性規劃”。
《基於約束最佳化問題的模式搜尋方法的研究》是依託南京大學,由吳婷擔任項目負責人的數學天元基金項目。項目摘要 對於很多實際套用中的約束最佳化問題,尤其是管理科學中遇到的部分問題,很難給出顯式函式表達式,只能對給定的自變數,觀測到相應...
《關於約束稀疏最佳化問題的理論、算法及套用研究》是依託西安交通大學,由徐鳳敏擔任項目負責人的面上項目。中文摘要 隨著信息處理技術的飛速發展和稀疏最佳化研究的深入,僅只考慮含稀疏約束的無約束稀疏最佳化模型已很難滿足實際需要(如:核密度...
大規模矩陣錐約束最佳化問題是最最佳化研究領域中的重要問題之一,在數值最佳化、魯棒最佳化、投資組合最佳化以及統計學理論等領域有著極其廣泛和重要的套用。現有的方法只能處理在對於中小規模的對稱矩陣問題,因此深入研究大規模的矩陣(特別是非對稱...
第1章 最最佳化方法的一般概念 1.1 目標函式、約束條件和求解方法 1.2 靜態最最佳化問題與動態最最佳化問題 1.3 線性規劃和非線性規劃問題 1.4 最最佳化方法在控制領域中的套用 習題 第2章 非線性規劃 2.1 一元函式的極小化 2....
項目按照申請書計畫進行,在Lp正則化的理論和數值算法及其套用方面取得了如下成果:1. 研究了Lp正則化問題的幾個理論問題:獲得了約束Lp正則化問題解的最優性條件(必要條件、充分條件). 該條件是通常約束最最佳化問題的最優性條件的一種...
項目擬結合求解PDE的區域分解和多尺度技術以及求解有限維變分不等式和最最佳化問題的有效算法設計求解上述問題的高效算法。特別是擬結合近二十年備受關注的求解有限維變分不等式等價的半光滑方程組的數值算法,如半光滑Newton型算法。項目擬建立...
4.7.4 複合最最佳化問題 4.8 Holder穩定性情形的二階分析 4.8.1 最優值函式的上二階近似 4.8.2 最優解的下估計與展式 4.8.3 Lagrange乘子空集 4.8.4 二階正則問題的Holder展開式 4.9 輔助結果 4.9.1 等式約束問題 4...
由於現代科學技術的高速發展,大數據分析與套用、科學與工程計算、物理與工程設計、經濟與金融分析等各領域提出一系列大規模(超大規模)面向實際套用的複雜數學最佳化問題。為了促進數據與套用驅動的數學最佳化理論、算法及其套用研究,本項目擬搭建...
2.6 用Mathematica求解無約束最最佳化問題 第3章 約束最最佳化的理論 3.1 約束最最佳化問題與Lagrange乘子 3.2 一階最優性條件 3.2.1 可行方向集與幾何最優性條件 3.2.2 Kuhn-Tucker條件 3.3 二階最優性條件 第4章 二次規劃 4...
本項目的研究將大量涉及到集值分析、非光滑分析、變分分析等領域的理論和工具,相關研究成果既可以豐富和發展最最佳化理論和方法,也可以廣泛用於求解現實世界提出的多種最最佳化問題,尤其是退化型的問題。結題摘要 求解約束最最佳化問題的一個...
第3章 無約束最最佳化方法 3.1 無約束最最佳化問題的最優性條件 3.2 最速下降法 3.3 Newton法 3.4 共軛方向法和共軛梯度法 3.5 擬Newton法 3.6 Powell方向加速法 習題 第4章 約束最最佳化方法 4.1 約束最最佳化問題的最優性...
《經濟管理中的均衡及帶均衡約束的最佳化問題》是依託湖南大學,由周叔子擔任項目負責人的面上項目。中文摘要 本項目研究社會經濟若干領域的均衡問題,建立其變分不等式模型,探討均衡模式的定性性質、可行的政策干預和相應的快速算法;同時還...
我們還研究了錐約束凸最佳化問題及其相關問題,如帶函式約束的變分不等式問題和極值最佳化問題的(廣義)弱尖銳性解。最後,我們還研究了向量最佳化中真擾動映射的二階相依導數的靈敏性和穩定性。
無約束條件的最最佳化問題是有約束條件的最最佳化問題的特例。實際問題一般都有資源限制,所以大部分最最佳化問題都是有約束條件的最最佳化問題。最最佳化問題根據決策變數在目標函式與約束條件中出現的形式可分為線性規劃問題和非線性規劃問題。如果...
庫恩-圖克條件,求解受不等式約束的最最佳化問題的充分和必要條件。庫恩-圖克條件是一個非線性規劃問題有最最佳化解法的一個必要和充分條件,用於求解受不等式約束的最最佳化問題。在求解受等式約束的最最佳化問題時一般用拉格朗日函式的方法求解,...
SQP( sequence quadratic program)是運籌學定義的縮寫。序列二次規劃(SQP)算法是求解中小規劃約束最最佳化問題的一類有效算法 思想 在問題的某個近似解x、處,解一個或幾個二次規划子問題,再通過這些子問題的解,去尋找更好的近似解....
