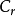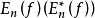線性逼近

線性逼近是對逼近工具的一種劃分概念。代數多項式逼近、三角多項式逼近、插值逼近等是線性逼近的一種，而另一種是藉助線性運算元的逼近，也即用來逼近函式的工具與函式的關係是線性的，人們亦稱它為線性逼近。

基本介紹

• 中文名：線性逼近
• 外文名：linear approximation
• 適用範圍：數理科學

簡介

線性逼近是對逼近工具的一種劃分概念。

設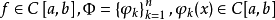，討論用 Φ 的元素的線性組合

對 f 的逼近，常常被稱為線性逼近。

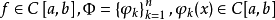
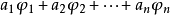
例如，代數多項式逼近、三角多項式逼近、插值逼近等。這是線性逼近的一種，而另一種是藉助線性運算元的逼近，也即用來逼近函式的工具與函式的關係是線性的，人們亦稱它為線性逼近。例如，傅立葉和及由其產生的種種線性平均的逼近、插值多項式的逼近等。除去上述兩個方面的逼近，人們常稱之為非線性逼近。例如，有理逼近、代數（或三角）多項式的最佳逼近運算元等都是非線性的。

聯合逼近

聯合逼近是同時逼近函式及其導數或用一個函式同時逼近多個函式的逼近，同時逼近函式及其導數的問題是可解的。

設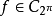有 r 階連續導數，則有不高於 n 階的三角多項式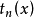，使得

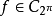
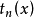
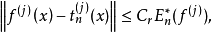
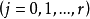
同樣，對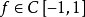，如果 f 有 r 階連續導數，則有不高於 n 次的代數多項式，使得

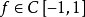
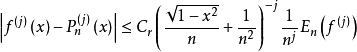
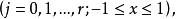
其中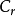是僅與 r 有關的正數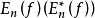，是 n 次（階）代數（三角）多項式對 f 對最佳逼近值。