代數多項式逼近

代數多項式逼近(approximation by algebraic polynomials)用代數多項式近似地表示連續函式。

基本介紹

• 中文名：代數多項式逼近
• 外文名：approximation by algebraic polynomials
• 適用範圍：數理科學

簡介

代數多項式逼近是用代數多項式近似地表示連續函式。

最佳逼近

記π_n為次數不高於n的代數多項式a₀+a₁x+...+a_nxⁿ的全體，這裡a_k(k=0,1,...,n)是實數。對於函式f∈C[a,b]，稱

為n次代數多項式對f在[a,b]上的最佳逼近值（度），也簡稱最佳逼近。

定義

這裡的下確界是能夠達到的，並且只有一個次數不高於n的代數多項式達到，記它為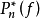，並稱它為函式f在區間[a,b]上的n次最佳逼近多項式。

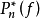
連續函式

函式y=f(x)當自變數x的變化很小時，所引起的因變數y的變化也很小。例如，氣溫隨時間變化，只要時間變化很小，氣溫的變化也是很小的；又如，自由落體的位移隨時間變化，只要時間變化足夠短，位移的變化也是很小的。對於這種現象，我們說因變數關於自變數是連續變化的。

連續函式在直角坐標系中的圖像是一條沒有斷裂的連續曲線。由極限的性質可知，一個函式在某點連續的充要條件是它在該點左右都連續。