簡介
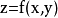
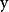



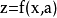
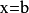

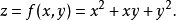
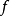
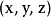
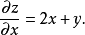
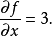
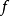
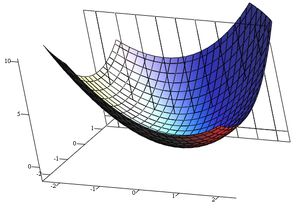 圖1 f=x2+xy+y2的圖像
圖1 f=x2+xy+y2的圖像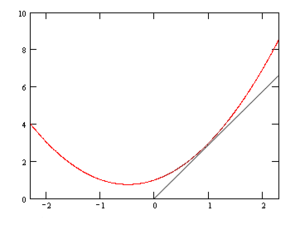
定義
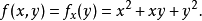
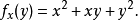
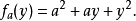
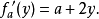
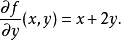
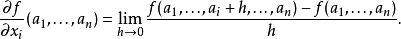
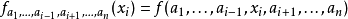
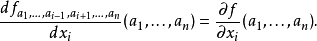
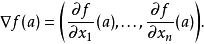
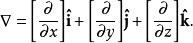
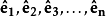
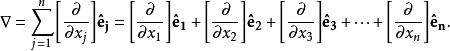
例子
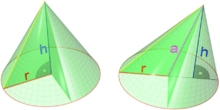 圓錐的體積與它的高度和半徑有關
圓錐的體積與它的高度和半徑有關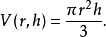
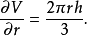
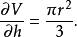
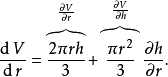
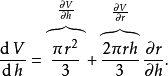
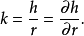
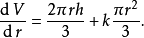
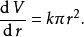
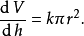
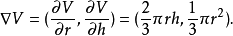
記法
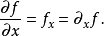
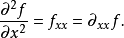
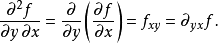
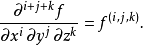
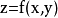
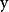



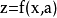
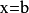
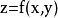
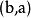

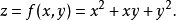
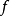
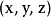
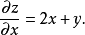
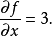
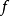
 圖1 f=x2+xy+y2的圖像
圖1 f=x2+xy+y2的圖像
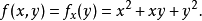
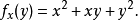
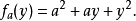
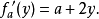
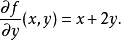
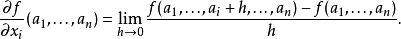
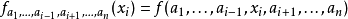
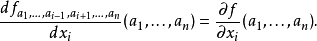
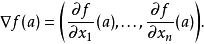
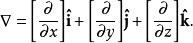
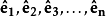
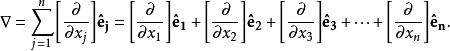
 圓錐的體積與它的高度和半徑有關
圓錐的體積與它的高度和半徑有關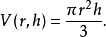
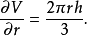
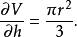
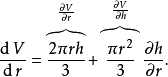
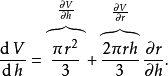
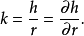
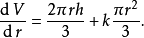
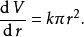
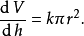
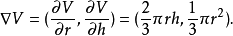
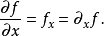
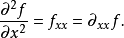
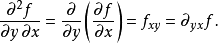
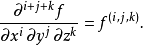
在數學中,一個多變數的函式的偏微商,又稱偏導數,是它關於其中一個變數的導數,而保持其他變數恆定(相對於全導數,在其中所有變數都允許變化)。偏導數在向量分析...
麥克斯韋關係式的主要作用是,實現用易於測量的狀態性質的偏微商,代替不易測量的狀態性質的偏微商,使人們可由此推導各種熱力學的關係。...
這時,存在函式R(x,y),它對x的偏微商為P,對y的偏微商為Q,結果方程R(x,y)=c(c為常數)將定義隱函式y,它滿足原來的微分方程。...
2.高階偏微商 3.全微分 4.全微分在近似計算中的套用 習題7.2 3方向微商與梯度 習題7.3 4複合函式及隱函式的微分法 1.複合函式的微分法 2....
含自變數、未知函式和它的微商(或偏微商)的方程稱為常(或偏)微分方程。未知函式為一元函式的微分方程,稱為常微分方程。未知函式為多元函,從而出現多元函式的偏...
習題6.2多元函式的偏微商與全微分6.2.1偏微商6.2.2全微分6.2.3高階偏微商6.2.4函式值的近似計算6.2.5誤差估計..7多變數函式的積分學...
曲面論中主曲率的仿射類似.設M是n+1維仿射空間中的局部嚴格凸的超曲面,二是位置向量,(u1,uz}...}u}})是局部坐標,Y是仿射法向量場.Y關於u'的偏微商可...
Δ δ delta /'deltə/ 變化量,屈光度,判別式,偏導(偏微商) Ε ε epsilon /'epsila:n/ 對數的基(底)數,偏心率,介電常數 Ζ ζ zeta /'zi:t...
2.2 標量場的偏微商與全微分2.3 張量分量場的偏微商與全微分2.4 矢量沿時間軸的平移操作2.5 標量場與張量分量場對時間T的協變微商...
這完全是由克萊因-戈登方程含時間的二次偏微商而帶來的。顯然幾率不能為負值。由於電荷密度可正可負,一般將 乘以電荷後表示電荷幾率密度,從而使理論自洽。[2] ...
化學勢就是吉布斯自由能對成分的偏微分,化學勢又稱為偏摩爾勢能。偏摩爾量都是系統的強度性質,強度性質在物理化學中也常可以寫成偏微商的形式,比如溫度T=dE/dS...
二級相變的特點是,兩相的化學勢和化學勢的一級偏微商相等,但化學勢的二級偏微商不相等。因此在相變時沒有體積變化和潛熱(即相變熱)。在相變點,兩相的體積、...
時域有限差分法的基本思想是用中心差商代替場量對時間和空間的一階偏微商, 通過在時域的遞推模擬波的傳播過程, 從而得出場分布。它最早由 K.S.Yee 於 1966 ...
6.1形式偏微商6.2可微同胚的復特徵與伸縮商6.3C1類擬共形映射的定義6.4Beltrami方程6.5複合映射的復特徵與伸縮商6.6共形模在C1類擬共形映射下的擬不變性...
類似的證明問題在熱力學中還有很多,通常的做法都要利用一些數學關係式,如偏微商的循環關係式和鏈式及倒置式、全微分式及其判別式、雅可比式等來解決,技巧也主要在...
它是對物體的物態方程或對物體的狀態方程如:f(T,p,V)=0在保持壓強p不變的情況下,體積V對溫度T求偏導而建立的偏微商關係。...
如果M是一個微分流形,其上的偏微商運算元可以通過局部坐標系定義。此時它的符號是M的餘切叢上的函式;對固定的M上的點,其符號是p的餘切空間上的齊次函式。此定義...
式中φ為擾動速度勢函式,φ的下標表示偏微商。這個方程既是非線性的(因為馬赫數Ma是速度的函式),又是混合型的。在超聲速區(Ma>1),它和波動方程一樣屬於雙曲...
通常狀態方程有3個變數,若某一變數保持不變,其他兩個變數之間可以建立微商關係(這就是偏微商),因而可由狀態方程求得反映系統的重要特性的三個係數。分別是體...
二、化學勢三、偏摩爾量【怎樣求解偏微商】精選題解(2)第三章 氣體【理想氣體熱力學】一、理想氣體的定義、狀態方程及過程方程二、理想氣體節流膨脹...
通常狀態方程有3個變數,若某一變數保持不變,其他兩個變數之間可以建立微商關係(這就是偏微商),因而可由狀態方程求得反映系統的重要特性的三個係數。分別是體...
F(x,y)=0中解出y,而把y看成是x的函式,在方程兩邊直接對x求微商 [1] ...兩邊再對x求偏微商,得 [2] 參考資料 1. 謝季堅,李啟文.大學數學:微積分...
