基本介紹
- 中文名:同倫映射
- 外文名:homotopic maps
- 領域:數學
- 學科:同倫論
- 對應類:同倫類
- 映射:連續映射
概念
拓撲學
拓撲空間
同倫
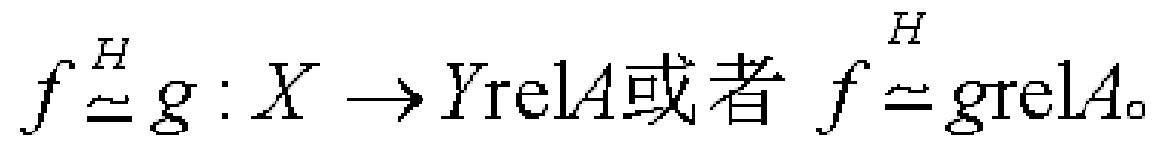
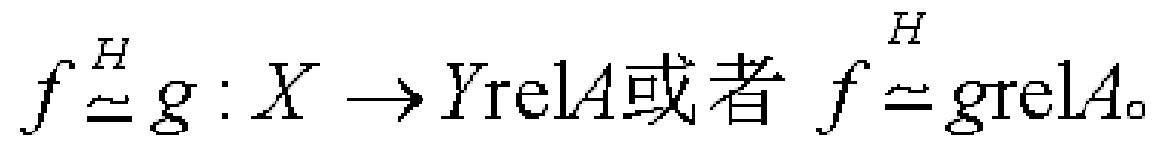
同倫映射(homotopic maps)是拓撲學中的重要概念。應該指出,映射的同倫關係是從拓撲空間X到Y的所有連續映射所成集合C(X,Y)上的一個等價關係,它將這些映射分成一些等價類,稱每個等價類為一個同倫類。研究映射的...
相對同倫 為定義高階基本群,必須考慮相對於一個子空間的同倫概念。這是指能在不變動該子空間的狀況下連續變化,正式定義是:設 是連續函式,固定子空間 ;若存在前述同倫映射 ,滿足:則稱 f,g 相對於K 同倫。若取 ,則回到原先...
《映射的同倫理論》是依託華南師範大學,由沈文淮擔任項目負責人的青年科學基金項目。項目摘要 進行了11種具有多重性質的實驗,取得了不同類型的數據,在全面分析傳統方法的基礎上,提出了4種創新性方法,可適應不同類型數據分析的需要;...
鏈同倫就是同調代數中來自拓撲學的一個重要概念,是從一個給定的鏈復形的所有鏈映射之間的一種等價關係。若h微由f到g的一個鏈同倫,這時稱f與g是同倫的。簡介 鏈同倫是從一個給定的鏈復形的所有鏈映射之間的一種等價關係。定義 ...
的同倫等價為 的同構。介紹 在數學的拓撲學領域中,同倫範疇是處理同倫問題時格外便利的範疇論語言。它的對象是拓撲空間,態射是連續函式的同倫類,這是商範疇的一個例子;由於同倫關係在映射的合成下不變,同倫範疇的定義是明確的。所有...
同倫群(homotopy group)是基本群的高維推廣。基本群是從單位閉區間I到拓撲空間X的閉路的同倫等價類和其運算得到的。定義 球面 同倫群 的元為帶基點映射Sⁿ→M的同倫類[Sⁿ,M]。圓盤 同倫群 的元為 的映射的同倫類,且將 映射至...
20世紀40年代原蘇聯數學家龐特里亞金給出從(n+k)維球到n維球的映射同倫分類,被稱為龐特里亞金類。20世紀50年代初,法國數學家塞爾提出了研究同倫群的新方法,利用纖維化的譜序列,取得了球面同倫群計算的突破性進展。20世紀50年代末...
同倫擴張(homotopy extension)是1993年公布的數學名詞,出自《數學名詞》第一版。定義 設i:A→X為拓撲空間範疇的連續映射,i₀:A→A定義為i₀(x)=(x,0)。若有f:X→Y與h:A→Y,滿足hi₀=fi,則存在 :X→Y,滿足 ,...
若(X;A,B,x₀)是空間的三聯組,使得(A,A∩B)是n連通的相對CW復形(n≥1),(B,A∩B)是m連通的相對CW復形,則由包含映射 誘導的映射 對於1≤r≤m+n是同構,對於r=n+m是滿同態。意義 同倫切除定理是同倫論的一個重要...
4.1 映射的同倫與空間的倫型 習題 4.2 道路·道路類 習題 4.3 基本群 習題 4.4 倫型不變性·簡單套用 習題 第5章 覆蓋空間 5.1 覆蓋空間 習題 5.2 覆蓋空間的基本性質 習題 5.3 咒維球面S”的基本群 習題 5.4 閉...
在本項目中, 我們將利用拓撲不動點理論方法,研究自映射的周期點的存在性和個數估計問題,以及不同周期的周期點之間的依賴關係。我們主要研究的一個關鍵量就是同倫最小周期集: 即映射同倫類中所有映射都存在的周期點的周期組成的自然數...
因此,那些與空間、所涉及映射的同倫類無關的定理或方法(比如同調、上同調或同倫理論本身)可能可適用到X,Y,f,這裡假設 以及 f事實上是子空間的包含。另外,這個構造更本質的吸引之處是它與通常心理的印象一個函式是將 X中的點...
是單連通CW復形,則存在一個(在同倫等價的意義下唯一)有理空間 以及映射 ,使得 誘導的所有同倫群的同態與 取張量積後都是同構。此空間 稱作 的有理化,同時 也是對於有理數的局部化,並稱作 的有理同倫型。通俗的說...
如果拓撲空間X到拓撲空間Y的映射同倫於一個其值域僅含單個點的映射,則稱該映射為非本質映射(inessential mapping)。不是非本質的映射稱為本質映射(essential mapping)。映入一個圓周(或n維球面)而其值域不是整個圓周(或球面)的映射是非...
在同倫映射下保持不變的空間內在性質稱為同倫型不變性質,如果它是數或代數結構則稱為同倫型不變數 。同倫不變數(homotopy invariant)是1993年公布的數學名詞。例子 (1).基本群是同倫型不變數 。公布時間 1993年,經全國科學技術名詞...
1、f同倫於g,若且唯若deg(f)=deg(g);2、對於任意給定的整數m,存在一個連續映射 ,使得deg(f)=m。同倫論中的定義 按照同倫論的術語,博特定理可以被陳述為:當2N≥n時GL(N,C)的同倫群為 由此可知,GL(N,C)的同倫群...
同倫於 ,那么其誘導同態相同:對所有的n>0。5、切除:設 是空間偶,U是X的子集,使得U的閉包包含在A的內部之中。那么包含映射 在同調群中誘導的是同構。6、維數:設P是單點空間,那么 對所有n≠ 0。7、正合:任何空間偶(X,...
進而,若對於(bEB,了Eb+)是同構,則了稱為向量叢同構,此時記為關於向量叢的一個重要事實是:若.f,:B>B是同倫映射,B'為仿緊空間,則由f,g分別決定的B'上的誘導叢.f' 與g'是叢同構.此定理稱為向量叢的同倫性質.
與常值映射同倫的映射稱為零倫的。若以C[X,Y]表示X到Y的一切連續映射之集,則同倫關係≃是C[X,Y]上等價關係,每個等價類稱為一個同倫類,同倫類的全體所成集記為[X,Y]。設Y是R的子空間,f,g:X→Y是連續映射,若對...
應該指出,映射的同倫關係是從拓撲空間X到Y的所有連續映射所成集合c(x,y)上的一個 等價關係,它將這些映射分成一些等價類,稱每個等價類為一個同倫類。研究映射的同倫分類問題是同倫論的基本內容之一。直觀地說,從拓撲空間X到拓撲...
當n= 0 ,這是道路連通分支間的映射,若假設X和Y是連通的,那么這映射不具有資料,可以忽略掉。若同態f都是同構,便稱f為一個弱同倫等價。懷特黑德定理說對於連通CW復形,一個弱同倫等價是一個同倫等價。注意 有一點要注意:單單...
與常值映射同倫的映射稱為零倫的。若以C[X,Y]表示X到Y的一切連續映射之集,則同倫關係≃是C[X,Y]上等價關係,每個等價類稱為一個同倫類,同倫類的全體所成集記為[X,Y]。設Y是R的子空間,f,g:X→Y是連續映射,若對...
懷特海定理 懷特海定理(Whitehead theorem)同倫論中一條重要的定理。懷特海定理斷言:若X,Y都是CW復形,則連續映射.f : X->Y是同倫等價若且唯若它是弱同倫等價.該定理表明,在CW復形的範疇中討論同倫論問題是非常合適的.
與常值映射同倫的映射稱為零倫的。若以C[X,Y]表示X到Y的一切連續映射之集,則同倫關係≃是C[X,Y]上等價關係,每個等價類稱為一個同倫類,同倫類的全體所成集記為[X,Y]。設Y是R的子空間,f,g:X→Y是連續映射,若對...
與常值映射同倫的映射稱為零倫的。若以C[X,Y]表示X到Y的一切連續映射之集,則同倫關係≃是C[X,Y]上等價關係,每個等價類稱為一個同倫類,同倫類的全體所成集記為[X,Y]。設Y是R的子空間,f,g:X→Y是連續映射,若對...
W.赫維茨1935~1936年間引進了拓撲空間的n維同倫群,其元素是從n維球面到該空間的映射的同倫類,一維同倫群就是基本群。同倫群提供了從拓撲到代數的另一種過渡,其幾何意義比同調群更明顯,但是極難計算。同倫群的計算,特別是球面的同倫群...
及同倫等價映射 及 的同倫逆 記 ,則 故X到自身的恆同映射是零倫的。命題 如果X是可縮空間,則 都是X的形變收縮核。證明 記 .由於X是可縮空間,因而r是同倫等價,又由於X是道路連通的,故從{x}到X的映射類只有一...
5.1 同倫映射 5.2 構造基本群 5.3 計算 5.4 同倫型 5.5 Brouwer不動點定理 5.6 平面的分離 5.7 曲面的邊界 第6章 單純剖分 6.1 空間的單純剖分 6.2 重心重分 6.3 單純逼近 6.4 復形的棱道群 6.5 軌道空間的...
