懷特黑德定理

在數學領域代數拓撲學的同倫論中，懷特黑德定理說，拓撲空間X和Y之間的連續映射f，誘導出所有同倫群之間的同構，則當X和Y是連通，並都有CW復形的同倫型的時候，f是同倫等價。

基本介紹

• 中文名：懷特黑德定理
• 學科：代數拓撲學
• 領域：數學
• 提出者：J.H.C.懷特黑德
• 提出時間：1949年

介紹

在數學領域代數拓撲學的同倫論中，懷特黑德定理說，拓撲空間X和Y之間的連續映射f，誘導出所有同倫群之間的同構，則當X和Y是連通，並都有CW復形的同倫型的時候，f是同倫等價。這條定理是J.H.C.懷特黑德在1949年的兩篇重要論文中證明，給出理由以他在論文所引入的CW復形概念作為研究對象。

定理敘述

更準確而言，假設給定CW復形X和Y，各有基點x和y。給定連續映射

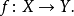
使得f(x) =y。考慮對於n≥ 1 的誘導同態

在此 π_n對n≥ 1 是第n個同倫群。當n= 0 ，這是道路連通分支間的映射，若假設X和Y是連通的，那么這映射不具有資料，可以忽略掉。若同態f_*都是同構，便稱f為一個弱同倫等價。懷特黑德定理說對於連通CW復形，一個弱同倫等價是一個同倫等價。

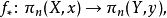
注意

有一點要注意：單單假設對每個n≥ 1都有π_n(X)與π_n(Y)同構，並不足以得出X和Y是同倫等價。定理中必需設有映射f:X→Y能同時誘導出所有同倫群的同構。例如令X=S²×RP³和Y=RP²×S³。那么X和Y有相同的基本群π₁，即是Z₂，也有相同的萬有覆疊空間，即是S²×S³；因此它們有同構的同倫群（覆疊空間的投影誘導出對所有n≥ 2的同倫群π_n的同構）。不過，它們的同調群不同（可以從屈內特公式看出）；所以X和Y不是同倫等價。

套用

懷特黑德定理對於一般拓撲空間不成立，甚至不對Rⁿ的所有子空間成立。例如，華沙圈（Warsaw circle）是平面的子集，所有的同倫群都是零，但是從華沙圈到一點的映射不是一個同倫等價。將這定理推廣至更一般空間的研究，是形狀理論的一部分。