雙曲不動點(hyperbolic fixed point、hyperbolic equilibrium point)可微映射具有局部結構穩定性質的不動點。它的常見定義是在一般黎曼流形上給出。
基本介紹
- 中文名:雙曲不動點
- 外文名:hyperbolic fixed point、hyperbolic equilibrium point
- 學科:數理科學
- 相關:黎曼流形
- 別名:雙曲臨界點、基本臨界點
簡介
地圖



流量




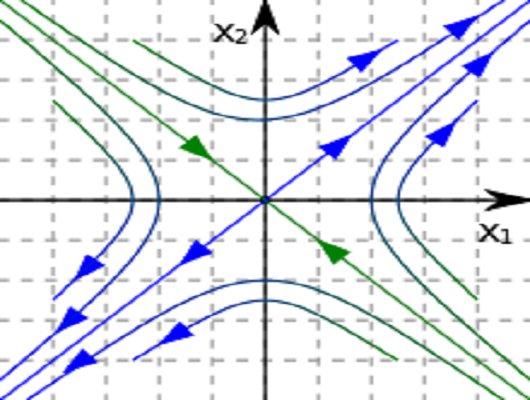
雙曲不動點(hyperbolic fixed point、hyperbolic equilibrium point)可微映射具有局部結構穩定性質的不動點。它的常見定義是在一般黎曼流形上給出。







雙曲周期點 雙曲周期點又稱雙曲不動點,是可微映射具有局部結構穩定性質的不動點。它的常見定義是在一般黎曼流形上給出。設U是黎曼流形M的開集,p∈U是f∈C(U,M)的不動點。若Df(p):TₚM→TₚM是雙曲線性映射,則稱p...
1)帶粘性的雙曲波動方程是典型的雙曲拋物方程,我們在解整體存在的基礎上,研究了此方程在小初值時奇數維空間解的逐點估計; 2)Benjamin-Bona-Mahony方程是研究在非線性擴散媒介中長波傳播的模型,是帶耗散結構的雙曲方程。此...
本項目擬對三維可幾何化流形及Haken流形自同胚的不動點及不動子群進行研究。結題摘要 本項目主要研究了三維流形自同胚的不動點及不動子群。1. 研究了雙曲流形的自同胚。通過研究,對姜伯駒先生1998年提出的一個猜想在雙曲流形的情形給...
(5)具有雙曲測度的微分流,在無不動點和法叢的Oseledec分解具有極限控制分解的條件下證明了此雙曲測度具有跟蹤性;(6)對C1微分同胚得到了一些正熵的充分條件,並對部分雙曲系統得到了熵的與不穩定子叢和穩定子叢維數相關的一個...
哈特曼定理亦稱哈特曼線性化定理。哈特曼定理(Hartman's theorem)它指出:C'微分同胚(C,向量場)f在其雙曲不動點(雙曲奇點)>p附近的動力學性質與其在p點的切映射}}Pf的動力學性質一樣.具體地說,設V是巴拿赫空間E中O點的鄰域,f ...
第九章 Rm中雙曲不動點的局部拓撲共軛分類 1 局部拓撲共軛的標準形式 2 局部拓撲共軛分類 第十章 雙曲不動點的穩定流形與不穩定流形 1 穩定集與不穩定集 2 穩定流形定理 第十一章 符號動力系統與“馬蹄”1 符號動力系統 2 移位...
基本集是動力系統研究的重要不變集之一。它是根據公理A系統譜分解的基本集所具有的動力學性質而抽象出來的概念。簡介 在動力系統的研究中,對基本集的理解一般認為它不是單獨的一個雙曲不動點(雙曲奇點)。基本集的作用在於它在很大...
本項目將研究退化異宿軌分岔,在連線異宿軌的雙曲不動點的穩定流形的維數不等時,找到多條異宿軌並存的各種參數條件;研究由退化異宿軌構成的異宿環分岔出同宿軌的問題,找到決定同宿軌存在的分岔函式,由分岔函式的可解性條件就...
3 雙曲不動點的穩定流形與不穩定流形 4 不變集與吸引子 5 拓撲共軛與符號動力系統 第三章 混沌 1 混沌的概念 2 蟲口模型 3 Henon映射 4 吸引子的特徵 5 時間序列的重構相空間 第四章 常微分方程基本理論 1 Rn中的常微分...
其次,我們將研究辛自同胚的雙曲不動點的拓撲橫截同宿軌道附近的動力學性態。由於缺乏幾何橫截相交性,因而不能構造馬蹄,傳統的微分動力系統的研究很少涉及這一方面的問題。我們將首先論證同宿軌道附近系統具有扭轉性質;以此為基礎,...
另外研究一類微分同胚在其雙曲不動點處光滑標準形問題。.基於標準形理論的套用,對凝血問題中一類非線性動力學模型在不改變系統動力學行為的前提下來研究其線性化問題,或使模型儘可能簡化,進一步討論動態系統的運行狀態及參數對系統穩定性...
第五章 遍歷理論 第六章 微分拓撲 第七章 結構穩定性 第八章 雙曲不動點的局部穩定性 第九章 雙曲不變集的結構穩定性 第十章 公理A與Ω穩定性 第十一章 Banach空間上的動力系統 第十二章 無窮維動力系統 參考文獻 ...
2.2 複合映射、壓縮映射與不動點 2.3 離散動力系統的基本概念 2.4 周期點、周期軌與沙可夫斯基定理 2.5 周期點的穩定性 2.6 雙曲不動點的穩定流形與不穩定流形 2.7 不變集與吸引子 2.8 拓撲共軛與符號動力系統 2.9 ...
本項目充分利用經典的正規形理論、Banach不動點定理,結合Hartman-Grobman拓撲線性化定理的泛函分析證明方法,來探討動力系統的線性化、正規形及一些相關問題。具體包括:探討R^n中微分同胚在雙曲不動點附近在不附加非共振條件下的Holder...
第26章 二維映射同宿點附近的動力學 第27章 三維自治向量場中雙曲不動點的同宿軌道 第28章 二維時間周期向量場中同宿軌道的Melnikov法 第29章 Lyapunov指數 第30章 混沌與奇異吸引子 第31章 雙曲不變集:混沌鞍點 第32章 耗散...
梯度向量域;可逆動態系統;漸進自控向量場;正規模;向量場不動點的分叉點;分叉圖的套用;Smale馬靴;符號動力系統;Conley-Moser條件或者“如何證明動力系統是混沌的“;二維映射同宿不動點附近的動力;三維自控向量域中雙曲不動點的...
