基本介紹
- 中文名:穩定流形
- 外文名:stable manifold
- 所屬學科:數學
- 所屬問題:動力系統(微分動力系統)
- 相關概念:穩定集,不穩定集等
基本介紹
穩定集與不穩定集

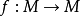
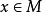
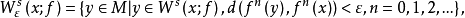



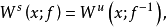


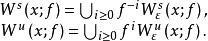




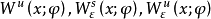



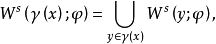



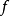










穩定流形定理
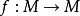

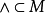
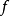
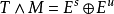


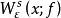
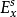



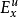






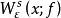








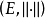



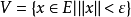



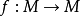
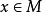
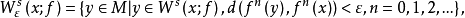



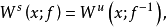


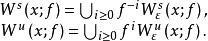




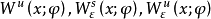



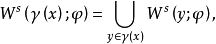



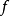










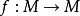

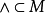
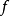
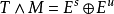


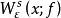
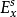



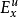






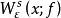








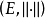



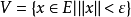

穩定流形(stable manifold)是微分動力系統的基本概念,它是微分動力系統研究的重要內容。穩定與不穩定流形是動力系統的不動點或周期軌附近當時間趨於無窮時會趨於該...
穩定集(stable set;stationary sets)有多個義項。一個是指多人合作對策的一種解集;另一個是指微分動力系統中與穩定流形相關的的穩定集;還指集合論中的一種...
中心流形定理(Center Manifold Theorem),控制理論中,考慮自治系統(時不變系統)dx/dt=f(x)。對其在平衡點(x*)線性化,則雅克比矩陣為 A=df/dt(x*)。中心流...
按一次近似決定穩定性(stability in the first approximation)是套用近似的線性...1和2表現的性質為典型的鞍點性質,它們給出了原點的局部穩定和不穩定流形[1] ...
3.5.1臨界轉速導致的穩定流形82 3.5.2氣動非線性造成的極限環運動86 參考文獻90 第4章有控旋轉彈的動態穩定性91 4.1彈體運動方程組的簡化91 4.2旋轉條件下執行...
雙曲不動點(hyperbolic fixed point、hyperbolic equilibrium point)可微映射具有局部結構穩定性質的不動點。它的常見定義是在一般黎曼流形上給出。...
第十六章雙曲集的穩定流形與不穩定流形1穩定集與不穩定集2穩定流形定理3穩定流形與不穩定流形的橫截相交第十七章公理A系統1公理A...
流形上的控制理論為非線性系統的研究提供了一條新的途徑,可用以研究非線性系統...第3章討論李雅普諾夫基本理論,給出各種穩定性的數學定義,並重點介紹李雅普諾夫...
強橫截條件亦稱幾何式橫截條件,結構穩定系統的基本條件之一。微分動力系統的研究...作為可微子流形橫截相交,稱一個公理 A 微分同胚滿足強橫截條件。羅賓...
黎曼流形,X是M上的Cr向量場,如果:1.X有有限個奇點和周期軌道,它們都是雙曲的;2.若σ1和σ2是X的奇點或周期軌道,那么σ1與σ2的穩定流形與不穩定流形是...
微分動力系統是微分流形上由常微系統或微分同胚生成的動力系統。研究的核心內容是結構穩定性和Ω穩定性的特徵性質。它起源於常微分方程結構穩定性的研究。雙曲周期...
那么存在一通有集羅CDiff <M>,使得對任意.f E } , .f的周期點是雙曲的,它們在非遊蕩集} <.f)中稠密,而且其穩定流形與不穩定流形是橫截相交的.這個...
