按一次近似決定穩定性(stability in the first approximation)是套用近似的線性系統研究更複雜系統穩定性的一種方法,即由最基本的線性(一次)系統出發研究能否決定更複雜系統的穩定性。
基本介紹
- 中文名:按一次近似決定穩定性
- 外文名:stability in the first approximation
- 所屬學科:數學
- 所屬問題:常微分方程穩定性理論
- 相關概念:Lyapunov函式存在性等
基本介紹,相關結論,
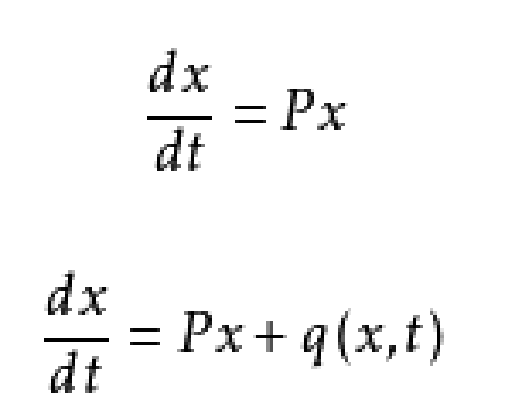
按一次近似決定穩定性(stability in the first approximation)是套用近似的線性系統研究更複雜系統穩定性的一種方法,即由最基本的線性(一次)系統出發研究能否決定更複雜系統的穩定性。
按一次近似決定穩定性(stability in the first approximation)是套用近似的線性系統研究更複雜系統穩定性的一種方法,即由最基本的線性(一次)系統出發研究能否決定更...
李亞普諾夫第一近似理論 利用一次近似判別非線性系統零解穩定性的理論。在原點將...的特徵根,而其他特徵根的實部非正,則原系統的穩定性由高次項f2 (x)決定 ...
6.2 解的穩定性6.2.1 Lyapunov穩定性的概念6.2.2 按一次近似判斷穩定性6.2.3 Lyapunov第二方法6.3 平面自治系統的奇點6.3.1 線性系統的奇點...
