雙曲不動點

雙曲不動點(hyperbolic fixed point、hyperbolic equilibrium point)可微映射具有局部結構穩定性質的不動點。它的常見定義是在一般黎曼流形上給出。

基本介紹

• 中文名：雙曲不動點
• 外文名：hyperbolic fixed point、hyperbolic equilibrium point
• 學科：數理科學
• 相關：黎曼流形
• 別名：雙曲臨界點、基本臨界點

簡介

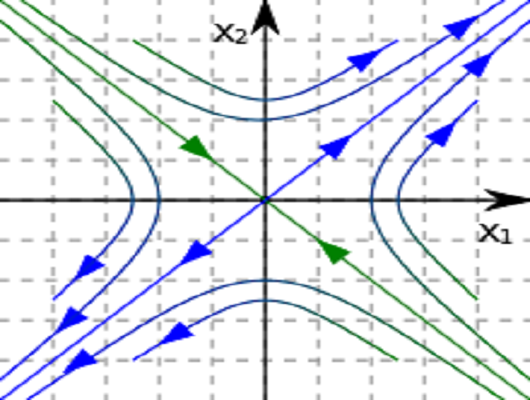
在動力系統的研究中，雙曲型平衡點或雙曲型不動點是一個沒有中心流形的固定點。在雙曲點附近，二維無耗散系統的軌道類似於雙曲線。這一般不成立。斯特羅加茲指出，“雙曲線是一個不幸的名字 - 聽起來應該是'鞍點'，但它已經成為標準。”幾個屬性擁有雙曲線點附近。

二維鞍點附近的軌道，雙曲平衡的一個例子。

• 一個穩定流形和不穩定流存在，
  
• 發生陰影，
  
• 不變集上的動力學可以通過符號動力學來表示，
  
• 一個自然的措施可以被定義，
  
• 該系統結構穩定
  

地圖

如果 是一個C映射，p是一個不動點，那么當雅可比矩陣為p時，稱p是雙曲不動點 在單位圓上沒有特徵值。

阿諾德的貓圖是固定點是雙曲線的地圖的一個例子：

由於特徵值給出

流量

讓 是具有臨界點p的C向量場，即F（p）= 0，並且令J表示在p處的F的雅可比矩陣。如果矩陣Ĵ具有零個實部沒有特徵值然後p被稱為雙曲線。雙曲不動點也可以稱為雙曲臨界點或基本臨界點。

哈特曼-格羅布曼定理指出，在一個動力系統的軌道結構附近雙曲線平衡點是拓撲等同於軌道結構線性化的動態系統。

示例

考慮非線性系統

（0，0）是唯一的平衡點。平衡線性化

這個矩陣的特徵值是對於α≠0的所有值，特徵值具有非零實部。因此，這個平衡點是一個雙曲平衡點。線性化系統的行為將類似於（0，0）附近的非線性系統。當α= 0時，系統在（0，0）處具有非雙曲平衡。