基本介紹
- 中文名:恆等映射
- 外文名:identical [identity] mapping
- 所屬學科:數學
- 所屬問題:集合(映射)
- 別稱:恆等函式
- 簡介:對任何元素,象與原象相同的映射
- 相關概念:映射,象,原象等
基本介紹
定義

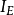

相關介紹



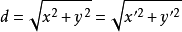
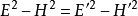
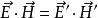


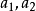

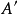
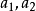
恆等映射的性質






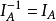
恆等變換




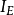




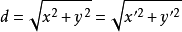
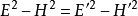
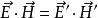


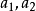

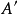
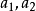






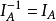


對任意集合A,如果映射f:A→A定義為f(a)=a,即規定A中每個元素a與自身對應,則稱f為A上的恆等映射(identical [identity] mapping)。...
設f:A→B是集合A到集合B上的一一映射,如果對於B中每一個元素b,使b在A中的原象a和它對應,這樣得到的映射稱為映射 f:A→B的逆映射,記作 1/f:B→A。...
如果拓撲空間X到拓撲空間Y的映射同倫於一個其值域僅含單個點的映射,則稱該映射為非本質映射(inessential mapping)。不是非本質的映射稱為本質映射(essential ...
零倫映射(null-homotopic map)是一類特殊的映射,設X,Y都是拓撲空間,若映射f:X→Y同倫於某常值映射f0:X→Y,則它稱為零倫的。從映射同倫觀點看,最簡單的...
調和映射(harmonic map)黎曼流形之間的一類十分重要的可微映射。數學上,在黎曼流形M和N之間的一個(光滑)映射,稱為調和映射。...
則稱f是A到B上的嵌入映射,記為A↪B。當A=B時,f就是恆等映射idA。在群論中,群A到B的嵌入有時也指A到B的單同態。詞條標籤: 文化 V百科往期回顧 詞條...
在數學的拓撲學中,閉映射是兩個拓撲空間之間的映射,使得任何閉集的像都是閉集。所以f: X → Y是閉映射,如果X中的閉集在f下的像都為Y的閉集。...
向量叢是流形切叢概念的抽象和推廣,它是微分拓撲學和代數拓撲學的重要研究對象。映射亦稱函式。數學的基本概念之一。也是一種特殊的關係。設G是從X到Y的關係,G...
度量空間亦稱距離空間。一種拓撲空間,其上的拓撲由距離決定。可擴映射(expansive map)是一類重要的動力系統。設(M,d)是一個度量空間,f:M→M是一連續映射,如果...
有理映射是代數簇上的有理函式概念的推廣。但是,它並不是集合意義下的映射。代數簇是代數幾何的基本研究對象。設k是一個域,域k上的代數簇就是一個整的、分離...
一致同構是指一致空間之間的同構。設(X,U),(Y,V )是兩個一致空間,若f:X→Y是單滿映射,且f和f-1都是一致連續的,則稱f為一致同構。並且稱空間X和Y為...
子流形是單浸入映射對應的流形間的關係。設M與N是兩個微分流形,φ:M→N是C∞映射,若φ是單射,且φ是浸入,則稱(M,φ)是N的子流形。或等價地定義為:M...
定義介紹 剛體布爾代數(rigid Boolean algebra)恆等映射id:是其惟一的自同構的布爾代數一個布爾代數B是剛體的,若且唯若在B中沒有非零不相交元素具有同構的相對...
度結構的自同構(automorphism of degrees'structure)遞歸論的基本概念之一指度結構到其自身的一一保序映射.若f為羅~少的一一映射,且對任何x,yE},x<yHf(x)<f...
