基本介紹
- 中文名:零倫映射
- 外文名:null-homotopic map
- 屬性:一類特殊的映射
- 定義:同倫於常值映射的映射稱為零倫的
- 所屬學科:數學(代數拓撲學)
- 相關概念:同倫,常值映射,可縮空間等
基本介紹,同倫的定義,零倫的定義,相關概念及性質,
基本介紹
同倫的定義
令X,Y是兩個空間,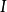 是單位區間
是單位區間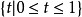 ,兩個映射
,兩個映射 是同倫的(記作:
是同倫的(記作: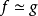 ),如果存在一個連續映射
),如果存在一個連續映射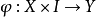 使得
使得 。直觀上,可以把t看成時間參數,
。直觀上,可以把t看成時間參數,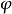 是從映射
是從映射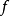 到映射
到映射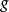 的一個連續變形,使得
的一個連續變形,使得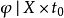 是
是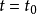 時的形變位置。也可以說,
時的形變位置。也可以說,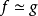 ,是指存在一個連續的單參數映射族
,是指存在一個連續的單參數映射族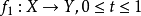 ,它以
,它以 為初始位置,以
為初始位置,以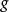 為終止位置。
為終止位置。
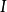
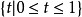

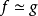
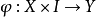

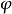
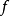
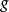
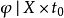
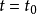
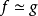
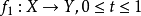

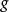
零倫的定義
例1 令Y是 的一個凸集,X是任意空間。則每個
的一個凸集,X是任意空間。則每個 都是零倫。因為,任選
都是零倫。因為,任選 ,定義
,定義 。則它是把X的每個點
。則它是把X的每個點 送到聯接
送到聯接 和
和 的線段上的某個點,而這個點分這個線段為
的線段上的某個點,而這個點分這個線段為 之比,
之比, 是連續的,並且
是連續的,並且 ,即
,即 和常映射同倫。
和常映射同倫。











相關概念及性質
可縮空間(contractible space)是一類特殊的空間,在同倫型的意義下,最簡單的空間是和由一個點組成的空間(即單點空間),有相同的同倫型的拓撲空間,稱為可縮空間,它和零倫映射有著密切關係。
一般地,說一個空間Y是可縮的,如果 是零倫的。並且,在這種情況下,對於每個空間X和每個連續映射
是零倫的。並且,在這種情況下,對於每個空間X和每個連續映射 都是零倫的。因為,若
都是零倫的。因為,若 是Y的一個收縮,則
是Y的一個收縮,則 就是
就是 的一個零倫.
的一個零倫.





例2 如果X是 中一個凸集,Y是任意空間,則同樣有每個
中一個凸集,Y是任意空間,則同樣有每個 是零倫。因為,取定
是零倫。因為,取定 ,定義
,定義 ,則
,則 連續,並且X的像收縮到
連續,並且X的像收縮到 。
。






一般,若X是可縮的,則對任何空間Y,每個連續映射 都是零倫;因為,若
都是零倫;因為,若 是恆等映射
是恆等映射 的零倫,則
的零倫,則 就是
就是 的一個零倫。
的一個零倫。





例3 注意:零倫映射之間不一定是同倫;實際上,常映射之間就不一定同倫:若X連通,Y不連通, 位於Y的不同連通支中,則常映射
位於Y的不同連通支中,則常映射 和
和 就不同倫,因為
就不同倫,因為 是連通的。
是連通的。




例4還必須注意,在考慮兩個映射 的同倫時,空間Y必須是固定不變的。假定允許Y任意擴大,則任意兩個映射
的同倫時,空間Y必須是固定不變的。假定允許Y任意擴大,則任意兩個映射 都可以是同倫的。比如,我們用
都可以是同倫的。比如,我們用 把
把 貼上到Y,(此處
貼上到Y,(此處 )得到
)得到 。若
。若 是粘合映射,則
是粘合映射,則 就是
就是 到
到 的在
的在 中的同倫。
中的同倫。











按照例1和例2,定義在 上的所有映射和所有到
上的所有映射和所有到 中的映射都是零倫的,但只要把
中的映射都是零倫的,但只要把 換成稍微複雜一點的空間
換成稍微複雜一點的空間 ,則兩個結論都是錯的:在n=0的情況,顯然
,則兩個結論都是錯的:在n=0的情況,顯然 不是零倫。
不是零倫。





然而,我們有以下命題:
(1) 若X是任意空間, 是兩個連續映射,使得
是兩個連續映射,使得 和
和 不是對徑點,則
不是對徑點,則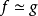 。特別,一個連續非滿射
。特別,一個連續非滿射 總是零倫的。
總是零倫的。



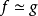

(2) 令Y是任意空間, 連續,則
連續,則 有一個連續擴張
有一個連續擴張 。
。