在微積分學中,一個實變數函式是可導函式,若其在定義域中每一點導數存在。直觀上說,函式圖像在其定義域每一點處是相對平滑的,不包含任何尖點、斷點。
可導性與連續性
魏爾斯特拉斯函式
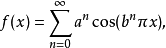

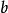

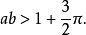
可導函式類
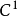
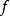


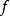
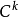
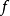
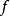
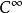

高維可導性
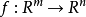



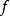
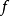
例子
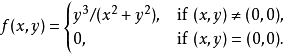
複函數的可導性


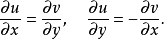

流形上函式的可導性
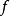

在微積分學中,一個實變數函式是可導函式,若其在定義域中每一點導數存在。直觀上說,函式圖像在其定義域每一點處是相對平滑的,不包含任何尖點、斷點。
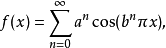

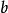

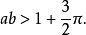
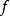
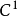
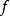


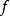
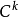
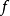
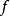
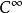

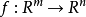



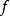
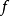
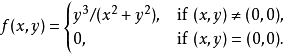


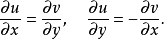


在微積分學中,一個實變數函式是可導函式,若其在定義域中每一點導數存在。直觀上說,函式圖像在其定義域每一點處是相對平滑的,不包含任何尖點、斷點。...
函式可導的充要條件:左導數和右導數都存在並且相等。可導函式可導與連續的關係 編輯 定理:若函式f(x)在 處可導,則必在點 處連續。...
在數學分析的發展歷史上,數學家們一直猜測:連續函式在其定義區間中,至多除去可列個點外都是可導的。也就是說,連續函式的不可導點至多是可列集。 ...
在微積分學中,可微函式是指那些在定義域中所有點都存在導數的函式。可微函式的圖像在定義域內的每一點上必存在非垂直切線。因此,可微函式的圖像是相對光滑的,...
可導性如果y=f(x)在(a,b)內可導並且在A+和B-處的導數都存在,則稱y=f(x)在閉區間[a,b]上可導。定理如果函式y=f(x)在點x處可導,則函式y=f(x)...
在數學中,魏爾斯特拉斯函式(Weierstrass function)是一類處處連續而處處不可導的實值函式。這個函式得名於它的發現者卡爾·魏爾斯特拉斯。歷史上,魏爾斯特拉斯...
次導數、次切線和次微分的概念出現在凸分析,也就是凸函式的研究中。設f:I→R是一個實變數凸函式,定義在實數軸上的開區間內。這種函式不一定是處處可導的,...
求導是數學計算中的一個計算方法,它的定義就是,當自變數的增量趨於零時,因變數的增量與自變數的增量之商的極限。在一個函式存在導數時,稱這個函式可導或者可微分...
相應地函式取得增量Δy=f(x0+Δx)-f(x0);如果Δy與Δx之比當Δx→0時極限存在,則稱函式y=f(x)在點x0處可導,並稱這個極限為函式y=f(x)在點x0處...
若當中的G為一個普通的可導函式g,則上式化為泛函導數確定的泛函導數 編輯 有一類常見的泛函,能表示成一個函式及其導數的積分的形式。對於這類泛函,可以給出一...
當函式 z=f(x,y) 在 (x0,y0)的兩個偏導數 f'x(x0,y0)與 f'y(x0,y0)都存在時,我們稱 f(x,y) 在 (x0,y0)處可導。如果函式 f(x,y) 在...
