基本介紹
- 中文名:處處連續處處不可導函式
- 所屬科目:數學
- 性質:函式
- 構造者:Weierstrass
可導誤區
介紹

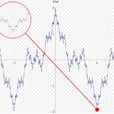

在數學分析的發展歷史上,數學家們一直猜測:連續函式在其定義區間中,至多除去可列個點外都是可導的。也就是說,連續函式的不可導點至多是可列集。 ...
處處不連續函式是數學名詞,是指在其定義域上的每一點都不連續的函式。狄利克雷函式是處處不連續函式的一個例子。...
在數學中,魏爾斯特拉斯函式(Weierstrass function)是一類處處連續而處處不可導的實值函式。這個函式得名於它的發現者卡爾·魏爾斯特拉斯。歷史上,魏爾斯特拉斯...
在微積分學中,一個實變數函式是可導函式,若其在定義域中每一點導數存在。直觀上說,函式圖像在其定義域每一點處是相對平滑的,不包含任何尖點、斷點。...
一般所謂的病態函式,往往指處處連續但處處不可導的函式,如魏爾斯特拉斯函式(Weierstrass函式),它是由一個無窮級數定義的,可以直觀地想像它,就是一條連續的鋸齒狀...
狄利克雷函式(英語:dirichlet function)是一個定義在實數範圍上、值域不連續的函式。狄利克雷函式的圖像以Y軸為對稱軸,是一個偶函式,它處處不連續,處處極限不存在...
函式y=f(x)在x0點的導數f'(x0)的幾何意義:表示函式曲線在點P0(x0,f(...例如,魏爾斯特拉斯函式(Weierstrass function)就是一類處處連續而處處不可導的實...
4.2.2.6 處處連續但處處不可導函式存在嗎4.3 級數的發展與成熟4.3.1 級數及其最初面臨的困境4.3.2 用定義判定級數斂散性及其簡單套用...
2.1.6 函式的可導性與連續性的關係36小資料 處處連續函式可以處處不可導362.2 導數的四則運算與反函式的求導法則372.2.1 導數的四則運算法則37...
數學對象的反常性主要表現為:反常事實,如德國數學家魏爾斯特拉斯在1856年提出的一個處處連續又處處不可導的函式,就與人們的傳統認識 “連續函式至少在某些點處可...
外爾斯特拉斯基本因式,即魏爾斯特拉斯函式,在數學中,魏爾斯特拉斯函式(英語:Weierstrass function)是一類處處連續而處處不可導的實值函式。魏爾斯特拉斯函式是一種...
