向量叢

向量叢是一個幾何構造，對於拓撲空間(或流形,或代數簇)的每一點用互相兼容的方式附上一個向量空間，所用這些向量空間"粘起來"就構成了一個新的拓撲空間(或流形，或代數簇)。

一個典型的例子是流形的切叢：對流形的每一點附上流形在該點的切空間。或者考慮一個平面上的光滑曲線，然後在曲線的每一點附上和曲線垂直的直線；這就是曲線的"法叢"。

向量叢是纖維叢的一種。

基本介紹

• 中文名：向量叢
• 外文名：vector bundle
• 相關術語：法叢
• 屬於：向量叢是纖維叢的一種
• 例子：流形的切叢#
• 套用學科：幾何學

定義

一個實向量叢要包含下列空間跟映射：

• X（基空間(base space)）和E（全空間(total space)）為拓撲空間(或是流形等其他空間)
  
• 一個連續滿射π:E→X（稱作投影）
  
• 對X中的每個x，π（{x}）是有限維的實向量空間(稱作纖維(fiber))。
  

且這些空間跟映射要滿足以下相容性條件：對X中的每一點有一個開鄰域 包含這點，一個自然數n和一個同胚

使得:

對所有x∈U，v∈R均成立

固定x，映射　 　是兩個向量空間R和 π（{x}）之間的線性同構，這對每點x∈U都成立。

開鄰域U和同胚φ合起來叫做叢的局部平凡化。這表示映射π在局部看起來"像"U×R到U上的投影.

向量叢X×R稱為平凡，如果賦予這空間一個投影映射　X×R→X，也就是E=X×R整體上是X的乘積空間 。

每個纖維π（{x}）是一個有限維實向量空間，所以有在點x有一個維數d_x，由局部平凡化的性質可知函式　 在局部上是常數，也就是它在X　的每個連通的部分上為常數。如果它在X上是常數的話，我們把這個維數叫做向量叢的階。一階向量叢也叫線叢。

向量叢態射

一個從向量叢π₁:E₁→X₁到向量叢π₂:E₂→X₂的態射（morphism）是一對連續映射f:E₁→E₂和g:X₁→X₂使得

• gπ₁= π₂f
  
• 對於每個X₁中的x,由f誘導的映射π₁({x}) → π₂({g(x)})是一個向量空間的線性變換。
  

所有向量叢的類和叢的射組成了一個範疇。限制到光滑流形和光滑叢射，我們就有了光滑向量叢的範疇。

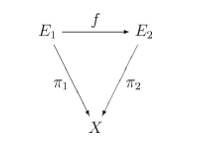
我們可以考慮有一個固定基空間X的所有向量叢組成的範疇。我們取那些在基空間X上為恆等映射（identity map）的射作為在這個範疇中的射. 也就是說，叢射滿足下面的交換圖：

（注意這個範疇不是可交換的；向量叢的射的核通常不能很自然的成為一個向量叢。）

截面

給定一個向量叢π:E→X和一個開子集U,我們可以考慮π在U上的截面,也就是連續函式s:U→E滿足πs= id_U.本質上，截面給U的每一點一個從附在該點的向量空間中所取的向量，取值要有連續性。

例如，微分流形的切叢的截面就是流形上的向量場。

令F(U)為U上所有截面的集合.F(U)總有至少一個元素：把V中的x映射到π（{x}）的零元的函式s.使用每點的加法和數乘，F(U)本身也成為了向量空間.這些向量空間的總和就是X上的向量空間的層。

若s屬於F(U)而α:U→R是一連續映射，則αs屬於F(U).我們可以看到F(U)是一個U上的連續實值函式的環上的模。進一步講，若O_X表示X上連續函式的層結構，則F是O_X-模的一個層。

不是O_X-模的每個層都是以這種方式從向量叢的導的：只有局部自由層可以從這種方法得到。（理由：局部的，我們要找一個投影U×R→U的一個截面，這些恰好是連續函式U→R,並且這一函式是連續函式U→Rn-元組.）

更進一步講：X上的實向量叢的範疇是等價於O_X-模的局部自由和有限生成的層的。

所以我們可以將向量叢視為位於O_X-模的層的範疇內；而後者是可交換的，所以我們可以計算向量叢的射的核。

向量叢的操作

兩個X上的在同一個域上的向量叢，有一個惠特尼和,在每點的纖維為那兩個叢的纖維的直積。同樣，纖維向量積和對偶空間叢也可以這樣引入。

變種和推廣

向量叢是纖維叢的特例。

光滑向量叢定義為滿足E和X是光滑流形，π:E→X是光滑映射，而局部平凡化映射φ是微分同胚的向量叢。

把實向量空間換成復的，就得到了復向量叢。這是結構群的約化的特例。也可以用其他拓撲域上的向量空間，但相對比較少見。

如果我們允許在局部平凡化中使用任意巴拿赫空間（而不僅是R），就可以得到巴拿赫叢。