誘導向量叢(induced vector bundle),亦稱向量叢的回退。由連續映射從一個向量叢按自然方式誘導產生的向量叢,這是構造新向量叢的常用方法之一。

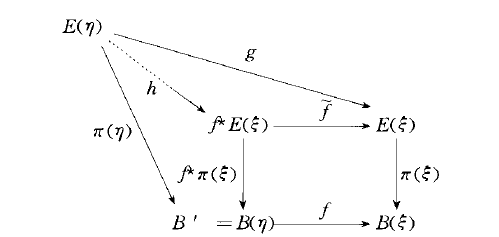
誘導向量叢(induced vector bundle),亦稱向量叢的回退。由連續映射從一個向量叢按自然方式誘導產生的向量叢,這是構造新向量叢的常用方法之一。


誘導向量叢(induced vector bundle),亦稱向量叢的回退。由連續映射從一個向量叢按自然方式誘導產生的向量叢,這是構造新向量叢的常用方法之一。...
誘導叢(induced bundle)是指從一個纖維叢經一個連續映射誘導出的一個新的纖維叢。纖維叢是坐標叢的一個等價類。由於每一個坐標叢都惟一地決定了一個纖維叢,故...
向量叢是一個幾何構造,對於拓撲空間(或流形,或代數簇)的每一點用互相兼容的方式附上一個向量空間,所用這些向量空間"粘起來"就構成了一個新的拓撲空間(或流形...
向量叢黎曼度量(Riemannian metric of vec-for bundle)對向量叢的一種刻畫。...... 若B是仿緊空間,則B上總存在黎曼度量.在正交向量叢的誘導叢上可以自然方式賦予...
向量叢值的外微分形式(exterior differentialforms valued in a vector bundle)流形上外微分形式的推廣.取值於向量叢的外微分形式.若}->M是M上一個有限維向量叢...
向量叢惠特尼和(Whitney sum of vectorbundle)亦稱向量叢的直和.指同一底空間上的兩個向量叢運用直和方式構造的新向量叢.設x,y分別是n維,k維向量叢,都以B為...
秩2向量叢是比線叢更複雜的向量叢。 直觀上說,就是底流形上每點處的2維向量空間的粘合。秩2向量叢局部上拓撲平庸, 但整體上未必拓撲平庸。...
第一變分公式是計算能量泛函的一階變分公式。若f:M→N是光滑映射,V∈Γ(f-1TN)是誘導向量叢f-1TN的一個截面,ft:M→N (-ε<t<ε)是滿足f0=f和...
若f:M→N是光滑映射,V∈Γ(f-1TN)是誘導向量叢f-1TN的一個截面,ft:M→N(-ε<t<ε)是滿足f0=f和 的單參數光滑映射族,則當V具有緊緻支集時,成立第...
