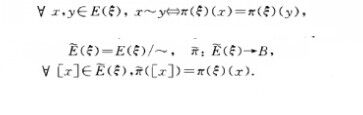
商向量叢(quotient vector bundle)一種常見的向量叢.它是由兩個同一底空間上的向量叢及其適合一定條件的叢同態構造的
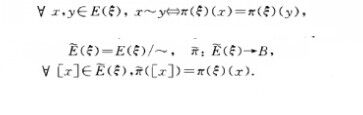
商向量叢(quotient vector bundle)一種常見的向量叢.它是由兩個同一底空間上的向量叢及其適合一定條件的叢同態構造的...
向量叢是一個幾何構造,對於拓撲空間(或流形,或代數簇)的每一點用互相兼容的方式附上一個向量空間,所用這些向量空間"粘起來"就構成了一個新的拓撲空間(或流形...
向量叢子叢指向量叢中全空間的子空間,它在一定條件下對於同一底空間按自然方式做成的向量叢。...
在數學中,帶有結構群 G(拓撲群)的纖維叢理論允許產生一個配叢,又稱配向量叢(associated bundle)的操作,將叢的典型纖維由 F1 變成 F2,兩者都是具有群 G 作用...
向量叢是流形切叢概念的抽象和推廣,它是微分拓撲學和代數拓撲學的重要研究對象。映射亦稱函式。數學的基本概念之一。也是一種特殊的關係。設G是從X到Y的關係,G...
平凡向量叢(trivial vector bundle)一類特殊的向量叢.若向量x=(E,p,B)有一個叢卡(B,p),則稱p是平凡向量叢.根據向量叢的同倫性質,任何可縮的仿緊空間上的...
秩2向量叢是比線叢更複雜的向量叢。 直觀上說,就是底流形上每點處的2維向量空間的粘合。秩2向量叢局部上拓撲平庸, 但整體上未必拓撲平庸。...
向量叢定向(orientation of vector bundle)具有定向性質的向量叢.設}_ (E,二,B)是n維向量叢,對於bEB,纖維E,,(作為向量空間)指定一個定向稱為x的一個定向,若...
向量叢黎曼度量(Riemannian metric of vec-for bundle)對向量叢的一種刻畫。...... 向量叢黎曼度量(Riemannian metric of vec-for bundle)對向量叢的一種刻畫。...
向量叢限制(restriction of vector bundle)一類特殊的向量叢.它是由一個已知的向量叢派生出來的.若(E,p,B)為向量叢,則B是向量叢,稱為在B上的限制,記為可看...
