參數變分指的是自變數變換時保持不變的自適應參數,套用於數學分析,深度學習等領域。
基本介紹
- 中文名:變分參數
- 套用領域:數學分析,深度學習
參數變分指的是自變數變換時保持不變的自適應參數,套用於數學分析,深度學習等領域。
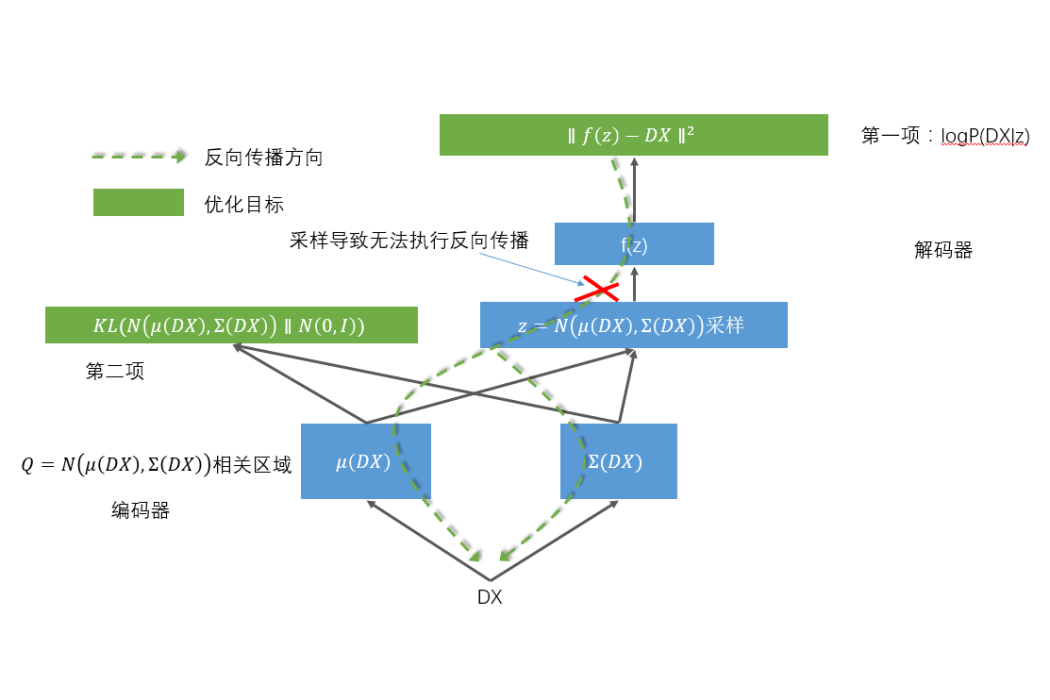
參數變分指的是自變數變換時保持不變的自適應參數,套用於數學分析,深度學習等領域。簡介對於普通的函式f(x),我們可以認為f是一個關於x的一個實數運算元,其作用是將實數x映射到實數f(x)。那么類比這種模式,假設存在函式運算元...
《參數變分系統的Lipschitz穩定性與最佳化問題》是依託哈爾濱師範大學,由宋文擔任項目負責人的面上項目。項目摘要 本項目旨在以變分分析為工具研究變分不等式系統的穩定性和敏感性分析問題,並套用於最佳化問題。通過對Banach空間中廣義多面體集(...
《極限分析中的參數變分原理及參數規劃法》是依託上海交通大學,由張柔雷擔任項目負責人的青年科學基金項目。項目摘要 在乾旱條件下,菌根混合接種較硬皮馬勃或VA菌根單獨接種更能促進毛白楊的高生長,縮球囊黴菌與硬皮馬勃混合接種增產幅度...
參數變分積分(parametric variational integral)是自變數變換時保持不變的一維積分。簡介 參數變分積分是自變數變換時保持不變的一維積分。參數變分積分的形式是其中c:[t₁,t₂]→M是N維流形M上的一條參數曲線,ċ是c的速度場。F...
改善波函式通常是通過一個含連續參數的特殊形式的波函式(,,,…)來實現的,這樣唕也就是這些參數的函式。式中代表體系的全部坐標,所猜測的波函式(,,,…)稱為嘗試波函式,變分參數(,,,…)是待定的。根據變分原理,由唕取極值,則...
§2.8 參數表示式 §2.9 歐拉方程的不變性 第三章 條件變分與變動邊界問題 §3.1 等周問題 §3.2 短程線問題 §3.3 微分方程作為附加條件 §3.4 自由邊界和自然邊界條件 §3.5 -階變分的一般形式 §3.6 變動邊界問題與...
《參變數變分原理及其在工程中的套用》是1997年科學出版社出版的圖書,作者是鐘萬勰、張洪 武、吳乘偉。內容簡介 本書系統闡述了參變數變分原理,並對彈塑性摩擦接觸問題、潤滑問題的基本思想及其數值求解方法進行了全面論述,還給出了大量...
《變分法》是工程力學專業本科生的專業課之一,是選修課,是《彈性力學》課程提高和延伸部分。用廣泛的變分方法來解決彈性力學的邊值問題,建立了彈性力學的幾個變分原理,從這些變分原理出發,用一致的方法導出各種類型彈性力學的平衡方程...
本書內容包括預備知識、固定邊界的變分問題、可動邊界的變分問題、泛函極值的充分條件、條件極值的變分問題、參數形式的變分問題、變分原理、變分問題的直接方法、力學中的變分原理及其套用以及含向量、張量和哈密頓運算元的泛函變分問題。其中...
弧長第一變分公式(first variation formula ofarc length)曲線族弧長泛函的一階導數公式.設Y(t) (aM是光滑映射,使得a(t,0)=Y(t),稱映射a為曲線Y的一個變分.對任意固定的、E(一:,:),若Y,,=a(t,s),a板t毛b,其長度...
變分 變分(variation)是1993年全國科學技術名詞審定委員會公布的數學名詞。公布時間 1993年,經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
變分問題(variational problem)是有關求泛函的極大值和極小值的問題。最早研究的重要變分問題有:1.最速降線問題:給定不在同一鉛垂線上的兩點A和B,求出連結A和B的一條曲線使其具有這樣的性質:當質點受重力作用沿著這條曲線由A下滑...
第一變分公式 第一變分公式是計算能量泛函的一階變分公式。若f:M→N是光滑映射,V∈Γ(fTN)是誘導向量叢fTN的一個截面,fₜ:M→N (-ε 的單參數光滑映射族,則當V具有緊緻支集時,成立第一變分公式:式中τ(f)為f的張力...
第一變分公式是計算能量泛函的一階變分公式。若f:M→N是光滑映射,V∈Γ(fTN)是誘導向量叢fTN的一個截面,fₜ:M→N(-ε 的單參數光滑映射族,則當V具有緊緻支集時,成立第一變分公式 式中τ(f)為f的張力場,表示N的黎曼...
變分貝葉斯估計(variational Bayesian inference)是統計推斷中變分方法(variational method)的套用之一,能夠以疊代方式在給定的變分族(variational family)中對機率模型的隱變數(latent variable)後驗分布進行局部最優估計。變分貝葉斯估計...
在信號處理中,變分模態分解是一種信號分解估計方法。該方法在獲取分解分量的過程中通過疊代搜尋變分模型最優解來確定每個分量的頻率中心和頻寬,從而能夠自適應地實現信號的頻域剖分及各分量的有效分離。釋義 變分模態分解的整體框架是變分...
變分原理的價值在於,可以根據微觀體系的物理特點確定波函式必須具有的性質並據此來建立含若干參數的嘗試函式,然後求出嘗試函式形式下的能量平均值,由該平均值取極值來定出所含參數的值,從而確定在所取形式下的最佳波函式和相應的能量。
變分導數 變分導數(variational derivative)是1993年公布的數學名詞。公布時間 1993年,經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
弧長第二變分公式(second variation formulaof arc length)刻畫弧長泛函在臨界點附近性態的重要公式.設Y(t) (a毛t毛b)是黎曼流形M中的一條測地線,t是弧長參數.若a;a,川X(一:,e)-.M是測地線Y的任意一個變分,則所謂弧長第...
就是變分不等式問題 的孤立解,即唯一局部解。對於變分不等式問題,我們有如下結論:定理1 變分不等式問題 有解的必要條件:如果向量 是變分不等式的一個解,並且存在梯度 ,使得梯度 ,和 線性獨立,那么,存在參數向量 ,使得...
第11章 根據修正的Hellinger—Reissner原理及具有一個參數的廣義變分原理建立的有限元模式(三)第12章 根據胡一鷲津(Hu—Washizu)原理所建立的有限元模式 第13章 根據修正的Hu—Washizu原理建立的有限元模式 第14章 根據更一般形式的...
發展一種新的區域邊界檢測濾波器,使變分模型自動決定在區域邊界點處的合理參數;(3)利用線性方程組解流型結構理論,結合Mean-Shift聚類算法,將圖像預分割為獨立配準區域,在每個區域中建立獨立變分模型。
本項目擬套用現代非線性分析的變分方法和拓撲方法等多種工具研究以下重要問題: 1.Bose-Einstein凝聚態和非線性光學中的變分問題,Schr?dinger 方程(組)解的存在性、性質,多參數分歧結構; 2.自由邊界問題和生物種群競爭極限系統中的...
《變分方法和幾何奇異攝動理論及其在微分方程中的套用》是依託江蘇師範大學,由林曉潔擔任項目負責人的青年科學基金項目。項目摘要 微分方程是研究力學、天文以及物理等自然科學的強有力工具。運用變分方法和幾何奇異攝動理論研究非線性微分方程...
非參數模型是指系統的數學模型中非顯式地包含可估參數。例如,系統的頻率回響、脈衝回響、階躍回響等都是非參數模型。定義 對比於確定已知模型結構中的各個參數,再通過理論分析得出的參數模型。非參數模型是直接或間接地從實際系統的實驗...
研究了非線性光學中的二次諧波模型,獲得了方程組基態解的存在性、部分唯一性和參數變化時解的分歧性質。 研究成果形成學術論文19篇,在15種國際重要期刊上發表,其中SCI期刊論文18篇,權威核心期刊論文1篇。研究結果揭示了具體變分問題的...
第5章系統探討了無窮維空間上的光滑和非光滑約束最佳化與均衡問題,第6章和第7章論述了變分分析在動態最最佳化和最優控制上的套用。其中第6章研究由常微分動力系統控制的最優控制問題;第7章討論分布參數控制系統,第8章提供了變分分析在...
(1)基於新型正則項,研究實用高光譜圖像光譜解混變分模型及其理論性質;(2)基於分而治之的分裂思想,研究適用於大規模高光譜圖像的高性能光譜解混算法及其理論性質;(3)研究高光譜圖像光譜解混模型中正則化參數的選取方法。
反問題基本理論——變分分析及在地球科學中的套用是一本2021年出版的圖書,由科學出版社出版 內容簡介 數學物理反問題(也包括地球科學反演)已成為套用數學發展和成長最快的領域之一.基於模型驅動的傳統科學和基於大數據分析的人工智慧領域,...
《應變速率矢量內積解法在軋制功率變分中的套用研究》是依託東北大學,由趙德文擔任項目負責人的面上項目。中文摘要 軋制是金屬成形的主要手段之一,軋制力矩與軋制力的精確值是現代軋機對軋制過程進行控制時預設定的關鍵參數,也是對具體鋼種...
