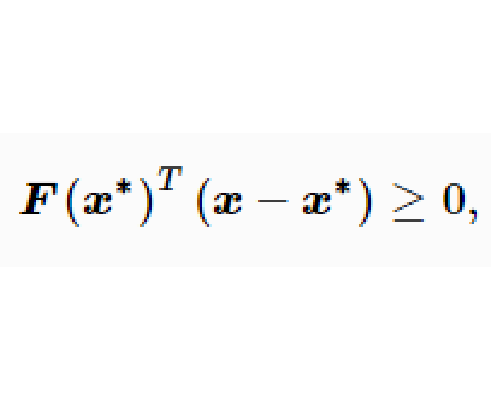定義
對於任一向量
,定義
向量函式
是連續的,
是
可微的,
是線性仿射的(Linear Affine)。其中
為如下的n×m矩陣
定義如下集合
則此不等式就是一個
變分不等式問題,並且
就是變分不等式的一個解。
變分不等式的解
解的定義
設
為變分不等式
的一個解,如果存在球鄰域
使得對任意的
,存在一個
使得
則稱
就是變分不等式問題
的孤立解,即唯一局部解。
對於變分不等式問題,我們有如下結論:
定理1
變分不等式問題
有解的必要條件:如果向量
是變分不等式的一個解,並且存在
梯度 ,使得梯度
,和
線性獨立,那么,存在參數向量
,使得
解的存在性及唯一性
定理2
變分不等式
有解的
充分條件:如果
是凹的,並且有
滿足定理1中的三個式子,則
就是變分不等式的一個解。
定理3
變分不等式問題
有唯一局部解的充分條件:在滿足定理2的條件基礎上,如果F是可微的,並且滿足:
,對於所有的y≠0,使得
定理4
如果
是強單調的,則定理3中三式成立,則變分不等式問題存在唯一解x。
變分不等式問題的求解方法
此處介紹求解變分不等式問題的一個著名的疊代算法,一般稱為鬆弛算法(Relaxation Algorithm)。
第二步:鬆弛化。求解如下最最佳化子問題
第三步:收斂性檢查。如果滿足收斂性,則停止;否則令n=n+1,轉第一步。
在鬆弛算法中,對於固定的y,由於函式Z(x,y)的Hessian陣
是對角陣,故在交通中常常也稱鬆弛算法為對角化算法,對應的最最佳化子問題被稱為對角化子問題。
在研究城市交通均衡配流問題時,當路段之間存在相互影響、而且這種相互影響是非對稱時,我們就可以採用上述對角化算法來求解這種路段相互影響的用戶均衡配流問題。