障礙問題(barrier problem)是對容許函式有不等式條件限制的變分不等式問題。來源於邊界固定的彈性薄膜在定義區域的某內部子域位於某給定物體(障礙)上方的平衡問題。
基本介紹
- 中文名:障礙問題
- 外文名:barrier problem
- 領域:數學
- 學科:變分學
- 函式:容許函式
- 性質:變分不等式問題
概念


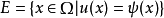
容許函式

障礙問題(barrier problem)是對容許函式有不等式條件限制的變分不等式問題。來源於邊界固定的彈性薄膜在定義區域的某內部子域位於某給定物體(障礙)上方的平衡問題。


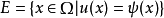

障礙問題(barrier problem)是對容許函式有不等式條件限制的變分不等式問題。來源於邊界固定的彈性薄膜在定義區域的某內部子域位於某給定物體(障礙)上方的平衡問題。...
(Attention Deficit Disorder)注意力缺陷障礙(ADD)的俗稱是兒童多動症,其發病原因很多,是兒童青少年時期長見病有的甚至廷續到成年。近年來由於環境、教育等因素,...
制約函式F(x,σ)=f(x)+σp(x)中的σp(x)稱為障礙項。障礙項的作用是在極小化過程中迫使疊代點靠近可行域,從而得到原問題的近似解。而且σ越大,近似程度...
障礙函式(barrier function)亦稱內懲罰函式、圍牆函式或碰壁函式,是一類制約函式。在數學領域約束最佳化中,障礙函式是一個連續函式,其中點的值隨著點到達最佳化問題的可行...
患者的注意興奮性的集中困難和緩慢,但是注意的穩定性障礙較小,患者對回答第一個問題完全正確,但對他接連不停地提出第二、第三個問題時, 他人回答就顯得緩慢,...
LD(learning disabilities)學習障礙症是西歐國家習慣的省略用語。...... LD一詞不包括因視覺、聽覺、動作障礙、智慧型不足或環境、文化、經濟等不利因素所造成的學習...
(1)往往在他人問題尚未問完時便急於回答。(2)往往難以靜等輪換。(3)常中斷或干擾其他人(如:插嘴或打斷別人的遊戲)。注意缺陷障礙治療 如果發現孩子有注意力缺陷...
閱讀障礙症簡單說來它是一種大腦綜合處理視覺和聽覺信息不能協調而引起的一種閱讀和拼寫障礙症。要特別注意區分它和那種因為智力低下而引起的閱讀障礙症,相反很多...
障礙表現法,就是指在描述情境時或在表現人物動作的過程中,如實地寫出種種阻礙人們實現既定目標、達到預期目的、擺脫不利處境的各種事物和事實的寫作方法。生活中一帆...
行為障礙是各種心理過程障礙的結果,可由各種原因產生。通常按其表現分為精神運動性抑制與精神運動性興奮兩類。...
溝通障礙是人際之間、團體之間交流意見、傳遞信息時所存在的困難。有如下幾種類型:(1) 語言障礙。語言是交流思想的工具,但不是思想本身,加之人們用語言表達思想的...
性障礙包括性生理功能及障礙及性心理障礙兩大類,性問題引起醫生的關心只是近數十年的事,在我國則還剛開始。由於性障礙常與心理因素有關,所以精神科醫生對此較早...
亦稱“情感障礙”或“心境障礙”。是指正常情感反應的誇張、混亂和減退。斷定情感反應是否正常或病態,需根據以下三個條件,即情感反應強烈程度、持續時間的久暫和是否...
市場障礙是指阻礙市場有序運行的問題、矛盾和摩擦。我國的市場障礙,是指在建立社會主義市場經濟過程中出現的有礙於建立統一開放、競爭有序的市場體系的問題,如區域...
傳播障礙是指在傳播活動過程中,由於傳播系統本身存在的結構性和功能性障礙,如不合理的傳播制度、不暢通的傳播渠道而導致的傳播行為受到障礙。...
路線障礙也稱線路障礙,顧名思義就是線路出現問題。常見的故障容易出現在母線與其他各設備的線路連線處接觸不良, 使得線路運行中斷。...
交流障礙是思想交流中產生的接受差閾。在日常生活中,人們說出的話是一種意思,可是在聽話人的理解中,它又變成另一種意思。同樣一種舉止、行為,在一個地區被認為...
註冊障礙指在註冊賬號或者其他需要註冊的產品的時候,發現自己的名字、身份證等信息已經被註冊的情況。...
但不包括由視覺、聽覺或運動系統缺陷,智力落後.情緒失常或由環境、文化或經濟狀況引起的學習問題。 學習障礙世界衛生組織(WHO)的定義 學習障礙是指從發育的早期...
《團隊協作的五大障礙》是2010年中信出版社出版的圖書,作者是(美)蘭西奧尼、華穎。...... 管理類暢銷書作家派屈克·蘭西奧尼針對團隊管理中五個普遍而又異常危險的...
分為社交心理障礙,社交功能社交障礙,社交焦慮障礙。分別表現為與人交往時(尤其是大眾場合下),會不由自主地感到緊張、害怕,以致手足無措、語無倫次,嚴重的甚至害怕...
概念應激相關障礙舊稱反應性精神障礙或心因性精神障礙,是指一組主要由心理、社會(環境)因素引起異常心理反應而導致的精神障礙。類別急性應激障礙(持續數小時至一周,...
(Attention Deficit Disorder)注意力缺陷障礙(ADD)的俗稱是兒童多動症,其發病原因很多,是兒童青少年時期長見病有的甚至廷續到成年。近年來由於環境、教育等因素,...
