基本介紹
- 中文名:非參數模型
- 外文名:Nonparametric models
- 學科:統計學
定義
非參數模型表示
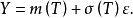
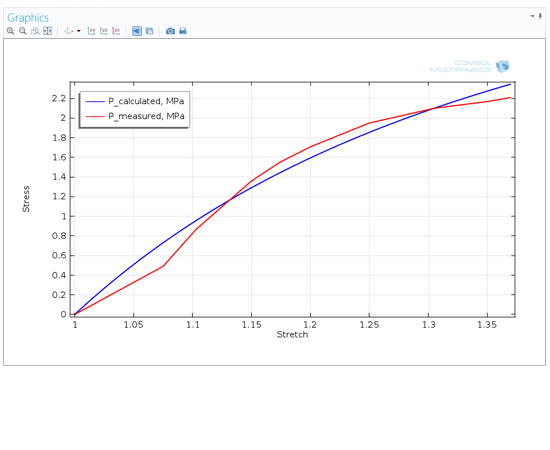
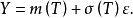
非參數模型是指系統的數學模型中非顯式地包含可估參數。例如,系統的頻率回響、脈衝回響、階躍回響等都是非參數模型。...
例如,系統的傳遞函式、頻率回響、脈衝回響、階躍回響等都是非參數模型。非參數模型通常以回響曲線或離散值形式表示。非參數模型的辨識可通過直接記錄系統輸出對輸入的...
《參數和非參數模型與估計及在能源經濟學中的套用》是2009年出版的圖書,作者是高煒宇。...
《非參數和半參數計量經濟模型理論》是2008年1月科學出版社出版的圖書,作者是葉阿忠。...
在這裡,d被稱為模型的維度。如果參數集合統計模型是非參數的 是無限的空間。如果統計模型同時具有有限維和無限維參數,則為半參數。形式上,如果d是維數 和n是樣本...
可加模型( additive model)是一種非參數模型,如果說二維散點圖的平滑是簡單線性回歸模型的一般化,那么加性模型就是多元回歸模型的一般化。加性模型非常具有靈活性...
分布參數模型是用各類偏微分方程描述系統的動態特性,而集中參數模型是用線性或非線性常微分方程來描述系統的動態特性。在許多情況下,分布參數模型藉助於空間離散化的...
《非參數與半參數統計》是2016年清華大學出版社出版的圖書,作者是孫志華、尹俊平、 陳菲菲、葉雪。...
機率圖模型學習算法分為參數學習與結構學習。基於機率圖模型學習分為機率網路的參數學習與結構學習算法,並根據數據集是否完備而分為確定性不完備,隨機性不完備各種...
《非參數統計:基於R語言案例分析》是柳向東在2015年2月編纂出版的圖書。...... 標準的參數方法強烈地依賴於對數據分布的假設,而非參數統計對模型要求甚少,不假定特...
《Tobit模型的半參數和非參數估計》是科學出版社出版的圖書,作者是周先波。...... 《Tobit模型的半參數和非參數估計》是科學出版社出版的圖書,作者是周先波。...
《全國大學生統計建模大賽獲獎論文選·從數據到模型》是一面鏡子,一個載體,字...5.流動性信息與資產收益:基於非參數模型的分析6.2009年上半年貨幣投放與未來...
《經濟、金融計量學中的非參數估計技術》是由科學出版社於2007年6月1日出版的圖書,作者是李竹渝,魯萬波,龔金國。...
侯忠生, 男, 1962年9月26日生。北京交通大學城市交通研究所教授,曾提出“無模型自適應控制理論”和“自校正控制系統的對稱相似結構設計構想”等。主持過非線性系統...
作為具有全貝葉斯特性(full Bayesian)的非參數模型,GPR可提供預測結果的後驗,且在似然服從常態分配時,該後驗具有解析形式,因此其是一個具有泛用性和可解析性的...
