克卜勒定律是德國天文學家克卜勒提出的關於行星運動的三大定律。第一和第二定律發表於1609年,是克卜勒從天文學家第谷觀測火星位置所得資料中總結出來的;第三定律發表於1619年。這三大定律又分別稱為橢圓定律、面積定律和調和定律。
基本介紹
- 中文名:克卜勒定律
- 外文名:Kepler's law
- 別名:克卜勒定律
- 提出者:克卜勒
- 提出時間:1618年
- 適用領域:航天
- 套用學科:天文學
克卜勒定律




數學推導
數學證明




































適用範圍
發展簡史
發現背景
行星軌道
克卜勒


發現過程



行星運動三大定律一般指本詞條
克卜勒定律是德國天文學家克卜勒提出的關於行星運動的三大定律。第一和第二定律發表於1609年,是克卜勒從天文學家第谷觀測火星位置所得資料中總結出來的;第三定律發表於1619年。這三大定律又分別稱為橢圓定律、面積定律和調和定律。














































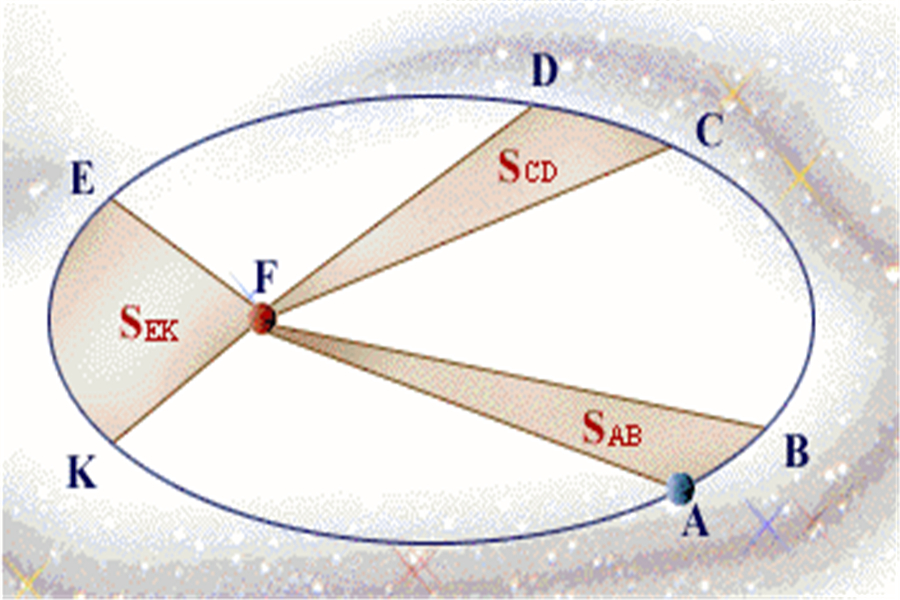
三大定律 對任何二物體(恆星與行星、行星與衛星、雙星系統…),如果它們間束縛力只有重力, 而且它們運動的軌道是橢圓或圓,則克卜勒三運動定律是必然的結果。所以,這裡呈現 的結果,不只是適用用行星系統。詳細內容 克卜勒第一定律 "行星繞太陽運行的軌道橢圓,太陽位在橢圓的焦點之一。"橢圓的半長軸以a 代表,半...
人類科學認識天體運動是從哥白尼(1473—1543)開始的,克卜勒(1571—1630)根據前人的天文觀測資料總結出了行星繞太陽運動的三大定律,被後人稱為克卜勒三定律。克卜勒和伽利略(1564—1642)之後,牛頓(1642—1727)提出了萬有引力定律和物體運動的三大定律(後人稱之為牛頓三定律),以此為基礎的牛頓力學是天體力學的基礎,...
克卜勒第一定律,也稱橢圓定律、軌道定律:每一行星沿各自的橢圓軌道環繞太陽,而太陽則處在橢圓的一個焦點上。克卜勒第一定律是由德國天文學家約翰尼斯·克卜勒提出的,他於1609年在他出版的《新天文學》科學雜誌上發表了關於行星運動的兩條定律,又於1618年,發現了第三條定律。在此定律以前,人們認為天體的運行...
運動定律 克卜勒是繼哥白尼之後第一個站出來捍衛太陽中心說、並在天文學方面有突破性成就的人物,被後世的科學史家稱為“天上的立法者”。克卜勒之所以留名青史的原因,是因為他發現了著名的《克卜勒行星運動三大定律》,這些定律是在沒有光學儀器的時代中,最後的重大發現。在他繼承了第谷的事業後,他對第谷留下來的...
這兩條定律刊布在1609年出版的《新天文學》(又名《論火星的運動》)中,該書還指出兩定律同樣適用於其他行星和月球的運動。套用領域 克卜勒第二定律,或者是用幾何語言,或者是用方程,將行星的坐標及時間跟軌道參數相連結。有效解決了對於天體運動規律的解釋。在研究天體的運動中,利用牛頓的力學和克卜勒三大定律的...
在人類歷史上,第一次預告水星凌日是“行星運動三大定律”的發現者,德國天文學家克卜勒(1571至1630年)。他在1629年預言:1631年11月7日將發生稀奇天象——水星凌日。當日,法國天文學家加桑迪在巴黎親眼目睹到有個小黑點(水星)在日面上由東向西徐徐移動。從1631年至2003年,共出現50次水星凌日。其中,發生...
天體運動中的勢能就是引力勢能。令無窮遠處勢能為零,則在半徑為r處的勢能為:M為中心天體質量。這當然是適用於任意軌道的。(3)綜上,我們可以得到機械能表達式:a為橢圓軌道半長軸。7.天體運動滿足克卜勒定律。天體運動釋義 天體運動,是在宇宙大爆炸發生後,形成空間天體運動的本原動力,也就是物質運動的動力源...
多四季論的理論是克卜勒的行星運動三定律和牛頓的萬有引力定律。他的立論根據是為世界各國科學家所公認的三大科學事實,即天體做多層次的周期性的運轉;氣候呈多層次地冷暖周期性地變化,冷暖之間有過渡期;生物周期性大滅絕。中心內容 地球在橢圓軌道上圍繞太陽公轉,形成小四季,周期為一年。在地球參與太陽系,圍繞...
重力常數又稱萬有引力常數,即萬有引力定律中表示引力與兩物體質量、距離關係公式中的係數。萬有引力常量是自然界中少數幾個最重要的物理常量之一。簡介 人類對引力的認識始於對行星運動的觀測。德國天文學家克卜勒(Johannes Kepler)根據丹麥天文學家第谷(Tycho Brahe)的大量翔實的觀測資料總結出行星運動三大定律,完美地...
歷史上出現過各種太陽、月球和大行星運動的假說,但直到1543年哥白尼提出日心體系後,才有反映太陽系的真運動的模型。克卜勒根據第谷多年的行星觀測資料,於1609~1619年間,提出了著名的行星運動三大定律,深刻地描述了行星運動,《天體力學》仍有重要作用。克卜勒還提出著名的克卜勒方程,對行星軌道要素下了定義。由此...
克卜勒發現了行星運動的三大定律,分別是軌道定律、面積定律和周期定律。這三大定律可分別描述為:所有行星分別是在大小不同的橢圓軌道上運行;在同樣的時間裡行星向徑在軌道平面上所掃過的面積相等;行星公轉周期的平方與它同太陽距離的立方成正比。這三大定律最終使他贏得了“天空立法者”的美名。同時他對光學、數學也...
(4)德國天文學家克卜勒(1571—1630)是哥白尼日心說的堅決擁護者。他經過十幾年的艱苦工作,發現了行星運動的三大定律:軌道定律、面積定律和周期定律。這三條定律的發現,在理論上證明和發展了哥白尼學說。也因此,克卜勒被稱為“天空立法者”。(5)伽利略(1564—1642)是科學革命過程中以及近代科學史上的一位...
《自然哲學的數學原理》的宗旨是從各種運動現象中探究自然力,再用這些力來解釋自然現象。貫穿全書始終的核心內容,是三大運動定律和萬有引力定律。全書共分五部分,第一部分是寫在正文前面的一個長長的“說明”,對書中用到的一些概念,諸如力、天體、力學、運動、物質的量等給出了定義和必要的說明;第二部分是“...
在人類歷史上,第一次預告水星凌日是“行星運動三大定律”的發現者,德國天文學家克卜勒(1571至1630年)。他在1629年預言:1631年11月7 日將發生稀奇天象——水星凌日。當日,法國天文學家加桑迪在巴黎親眼目睹到有個小黑點(水星)在日面上由東向西徐徐移動。從1631年至2003年,共出現50次水星凌日,其中,...
在牛頓之前,天體運動和地上運動是被分開來考慮的。伽利略提出了運動的相對性,運動的合成和自由落體的法則,笛卡爾討論了慣性原理的動量守恆法則;克卜勒提出了行星運動三定律。牛頓的主要工作是將天體和地上的運動研究成果統一起來,並從數學上給予適當的證明。《原理》給出了著名的牛頓運動三大定律以及引力和距離的平方...
第谷·布拉赫是天文史上的一位奇人。他對於星象的觀測,其精確嚴密在當時達到了前所未有的程度。其編纂的星表的數據甚至已經接近了肉眼解析度的極限,這讓人瞠目結舌。第谷的數據為其弟子——大名鼎鼎的克卜勒所運用,由此創立了著名的行星運動三大定律,成就了近代天文學的開端。第谷的鼻子 關於第谷,流傳著兩個八卦...
年輕的高斯卻有自己的看法。他認為,天文學是離不開數學的。如果沒有雄厚的數學知識,是不可能成為一個出色的天文學家的。在天文學發展史上,情況也正是如此。克卜勒正是憑藉著自己的數學才能,才發現了行星運動的三大定律。牛頓也是憑著淵博的數學知識,才發現了萬有引力定律。在高斯之前,著名數學家歐拉曾經研究出...
德國天文學家克卜勒提出了行星運動的三大定律,英國物理學家牛頓用力學的引力原理解釋克卜勒的行星運動定律,創立了天體力學。現代宇宙學最有影響的學說是大爆炸宇宙學。大爆炸宇宙學認為,宇宙早期溫度極高(在100億度以上),物質密度極大。在那裡,物質被壓縮成一個奇點,時間和空間都毫無意義。大約200億年前,發生“...
人造地球衛星繞地球運行遵循克卜勒行星運動三定律。(1)衛星軌道為一橢圓,地球在橢圓的一個焦點上。其長軸的兩個端點是衛星離地球最近和最遠的點,分別叫做遠地點和近地點。(2)人造地球衛星在橢圓軌道上繞地球運行時,其運行速度是變化的,在遠地點時最低,在近地點時最高。速度的變化服從面積守恆規律,即衛星...
對茫茫星空的觀測,導致劃分星座和編制星表,進而研究太陽、月球和各大行星在天球上的運動。當時的天體測量學既奠定了曆法的基礎,又確認了地球的自轉和公轉在天球上的反映,從而逐漸形成古代的宇宙觀。因此,早期天文學的主要內容就是天體測量學。根據浩瀚的天體測量資料,經過精心研究得出的克卜勒行星運動三大定律,為...
他在1687年發表的論文《自然哲學的數學原理》里,對萬有引力和三大運動定律進行了描述。這些描述奠定了此後三個世紀裡物理世界的科學觀點,並成為了現代工程學的基礎。他通過論證克卜勒行星運動定律與他的引力理論間的一致性,展示了地面物體與天體的運動都遵循著相同的自然定律;從而消除了對太陽中心說的最後一絲疑慮,...
另一方面,克卜勒根據第谷的30年天文觀測資料總結出行星運動的三定律(1609,1619)。I.牛頓繼承和發展了這些成果,提出了物體運動定律和萬有引力定律。他的成就收在1687年出版的《自然哲學的數學原理》中。他在本書中給出的運動三定律是:①第一定律:任何一個物體將保持它的靜止狀態或作勻速直線運動,除非有施加於...
在人類歷史上,第一次預告水星凌日是"行星運動三大定律"的發現者,德國天文學家克卜勒(1571至1630年)。他在1629年預言:1631年11月7 日將發生稀奇天象--水星凌日。當日,法國天文學家加桑迪在巴黎親眼目睹到有個小黑點(水星)在日面上由東向西徐徐移動。從1631年至2003年,共出現50次水星凌日,其中,發生在...
2.3 行星逆行與地心說 第3節 觀星有成 3.1 從地心說到日心說 3.2 火星的軌跡與三大定律 推薦主要閱讀資料5 小組討論題5 作業題5 第6講 站在巨人的肩膀上—克卜勒行星運動三定律與 萬有引力定律 第1節 微積分概覽——數學刻畫自然的威力 1.1 函式、極限——微積分的研究對象及工具 1.2 微分學和...
