簡介 地球繞太陽公轉 的軌道是一個橢圓,它的長直徑和短直徑相差不大,可近似為正圓。太陽就在這個橢圓的一個焦點上,而焦點是不在橢圓中心的,因此地球離太陽的距離,就有時會近一點,有時會遠一點。
1月初,地球離太陽距離最近,為1.471億千米,這一點叫做近日點。
7月初地球離太陽最遠,為1.52億千米,這一點叫做遠日點。事實上,當地球在近日點的時候,北半球為冬季,南半球為夏季,在遠日點的時候,北半球為夏季,南半球為冬季。在近日點
地球公轉 速度較快,在遠日點較慢。對於農曆而言,近日點附近是最難出現
閏月 的位置。
在近日點時,地球接受到的
太陽輻射 更強(距離近),地球整層大氣平均溫度在1月達到全年最高;但最低的溫度並不是在遠日點,而是在10月(偶爾也會在9月)。
事實表明(經過美國大氣中心NCEP資料計算),全球整層大氣平均風能通常在8月最大,4月最小。
速度計算 定律計算 在這箇中心力場的問題中,對於一個繞轉的物體,在運動過程中,
角動量 是守恆的,包括它在近日點和遠日點時,具體的說就是 L=MV(近)R(近)=MV(遠)R(遠)
對於具體一個的物體,M不變 ,V垂直於它於太陽的連線。
一顆
行星 距太陽最近的點。當對象為地球而非
太陽時 則使用“
近地點 ”一詞(perigee); periapsis用於公轉其他星體。(與遠日點相對)
天體軌道只能有一個近日點,而遠日點則可以沒有或有一個。
近日點相關公式計算 地球 :1月初 近日點
日地距離 1.471億千米 角速度61分/天 線速度30.3千米/秒
水星 :近日點在它的
軌道平面 上移動,每100年向前移動(天文學上稱為
進動 )5601"左右,比根據
牛頓定律 推算出來的值偏高43",這個值被稱為水星近日點反常進動。1859年,
海王星 的發現者——法國天文學家
勒威耶 (Urbain Le Verrier)在發現海王星的啟發下,大膽地提出這種現象是由於一顆未知的
水內行星 對水星的攝動引起的。同年便有人宣稱發現了水內行星,並起名為“
火神星 ”,一時間掀起了尋找火神星的熱潮。然而幾十年過去了,此夢一直未圓。於是人們構想各種因素來解釋這種複雜的進動,但始終沒有令人滿意的理論解釋。
名人計算 繼
牛頓 之後,1915年,偉大的科學家
愛因斯坦 建立了
廣義相對論 ,巧妙地解釋了水星的近日點進動現象:行星在繞太陽一周之後,它在軌道上的近日點將向前進去。廣義相對論揭開了水星近日點進動之謎,反過來,水星近日點進動又成為廣義相對論最有力的三個天文學驗證之一。另外兩個是,
日全食 時星光在太陽引力場中的彎曲以及
白矮星 光譜線紅移。
1859年,天文學家
勒威耶 發現
水星 近日點進動觀測值,比根據
牛頓定律 計算的理論值每百年快38角秒。1882年,
紐康 經過重新計算,得出水星近日點的多餘進動值為每百年快43角秒!他提出,有可能是水星因發出
黃道光 的彌散物質使水星的運動受到阻尼。1915年愛因斯坦在《用廣義相對論解釋水星近日點運動》計算了水星近日點的剩餘進動。
近日點與黃道平面 愛因斯坦1915年對水星的進動,提出公式,解出水星100年的進動為 43”。許多人以此作為支持愛因斯坦的理論的最重要證據之一!
愛因斯坦提出的公式為:Δω=24π^3*α^2/c^2T^2(1-e^2)
其中c為光速,T為軌道周期,α為半長徑,e為偏心率,ω為交進動。
太陽風 對此,
吳大猷 先生謹慎地寫道:“在
水星 之情形,觀察的結果,需先做許多校正(如受其他星星之干擾等)這些校正總值達5160” 之巨,剩餘43”實不及總值的百分之一。故理論與觀察結果之吻合,似不宜遂作定論。但按專家們的意見,則以為觀察是支持愛因斯坦的理論的。”上世紀六十年代,人們發現太陽風.一般認為太陽通過
太陽風 每年損失3X10-14M⊙!
愛因斯坦1915年計算顯然沒有包括太陽風的概念!
討論水星的進動,引入太陽風的概念意味之一是太陽每一百年對水星的引力至少減少3X10-12倍。
引入太陽風的概念意味之二是太陽風對水星的外推!依據
動量守恆定律 mv=M v’。 m為
水星 所受到的太陽風作用,v為太陽風速度; M 為水星質量, v’為水星速度變化。
水星公轉軌道數值約為579萬Km,水星公轉軌道扁率約為0.2056。水星半徑約為2439Km。球面
面積公式 S=4Π .R.R。水星公轉軌道球面面積約為421227.6x10ˆ12Km2。水星面積約為4672114.5km2,兩者之比為9.017x109ˆ。
太陽質量 約為1.99x10ˆ33g,水星質量約為3.303x102ˆ3g。考慮太陽系、
銀河系 等均為平面結構的事實,可以假定太陽風主要散失在太陽
赤道面 。加之考慮水星公轉軌道扁率、水星對太陽風的引力作用,對水星獲得的太陽風物質予以增大,乘以係數100。則得100年
水星 獲得的太陽風物質約為 3.32X10-20M⊙。
地球處太陽風的最大速度約為900 Km/S。太陽表面物質的最小脫離速度約為624 Km/S。取水星處太陽風速度約為780 Km/S。
將以上數值簡單代入公式mv=M v’,可得每百年v’約為7.84X10-5m/S。
太陽風引起的引力變化與外推作用之和對水星每百年 43”的進動相比不是可以忽略不計的!
要知道水星公轉周期約88
地球日 ,水星每百年的運動100x4.14x360x60x60與每百年 43”的進動相比也是天文數字!
當然,我開始考慮太陽風因素時,我曾構想做天體的“N體”計算。但隨著時間的變化,認識到這是現在無法做到的。
將太陽風因素引入 水星進動 的“N體”計算是否會支持愛因斯坦理論?
愛因斯坦1915年的水星進動計算很大程度上可以被認為是對
牛頓方程 進行係數調整以適應已知的43”! 因為水星進動 的“N體”精確計算的篇幅至少會是數以百萬字的,而不會只是一個普通論文篇幅!
觀點 根據
牛頓萬有引力定律 計算的水星近日點進動值與觀測值的分歧。1859年﹐法國天文學家
勒威耶 發現水星近日點進動的觀測值﹐比根據
牛頓定律 算得的理論值每世紀快38°﹐並猜測這可能是一個比水星更靠近太陽的水內行星吸引所致。可是經過多年的辛勤搜尋﹐這顆猜測中的行星始終毫無蹤影。紐康測定這個值為每世紀 43度。他提出﹐這可能是那些發出黃道光的瀰漫物質的阻尼所造成的。但是﹐這種假設又不能解釋其他幾顆行星的運動。於是紐康就懷疑萬有引力定律中的平方反比規律有問題。為了能同時解釋幾顆內
行星 的實際運動﹐紐康求出了引力應與距離的2+1.574×10次方成反比。19世紀末﹐
電磁理論 發展的早期﹐
韋伯 ﹑
黎曼 等人也都曾試圖用電磁理論來解釋
水星 近日點的進動問題﹐但均未能得出滿意的結果。
近日點經度分布 依據
牛頓 萬有引力定律計算所得的水星近日點進動理論值與實際觀測所得到的觀測值之間的差異所產生的分歧問題。1859年,法國天文學家U.J.J.勒威耶根據多次觀測發現所得到的水星近日點進動值要比按照牛頓萬有引力定律計算所得的理論值每世紀快38秒出現水星近日點反常進動他的這一發現引起了眾多天文學家的注意很多人對這一問題進行了研究和修正。進一步測定水星近日點進動的觀測值與理論值之差為每世紀43秒,於是有人懷疑牛頓萬有引力定律是否普遍適用。但長期得不到完滿的解釋。直至1915年,愛因斯坦根據他創立的廣義相對論原理對水星近日點的進動進行了計算他的計算值與按照牛頓萬有引力定律計算得到的值之差值為每世紀43″03。這個值與觀測值十分接近,從而成功地解釋了
水星 近日點反常進動。
進動值的分歧問題,成為天文學對廣義相對論的最有力的驗證之一。影響水星近日點進動的因素很多,任何微小的變動都會影響到對廣義相對論的驗證,因此,這個問題尚需要繼續研究。
近點進動 由於其他
大行星 (主要是木星)的攝動影響,地球公轉軌道的近日點也有進動現象,周期約為21000年,每年約1.03',也就是說每58年地球推遲一天到達近日點,比如公元1250年地球到達近日點的時間在冬至附近,而現在目前則是每年1月3日或4日到達近日點。
從長期來看,地球近日點的進動雖然微小,但也是造成地球氣候冷暖變化的重要因素之一。
南斯拉夫 天文學家
米蘭 科維奇(Milankovich)於1930年提出
地質時期 氣候變化與地軸傾斜度的變化、
地球軌道 偏心率 的變化和近日點的位置變化有關。
其它彗星 Swift-Tuttle
英仙座流星雨的
流星體 來自周期135年的Swift-Tuttle彗星(
斯威夫特彗星 ),當地球經過
彗星 軌道附近時,重力將這些從
彗核 散布出來的塵埃、碎粒吸引至地球,以高速沖向
大氣層 ,摩擦燃燒後發出短暫的光芒,就是我們所見的流星。較大的流星體其尾跡可在夜空中持續數分鐘之久。
1992年11月過近日點的 109P/Swift-Tuttle 彗星。下一次 le彗星要到2126年才會再度通過近日點。
貝內特彗星
1970年3月20日,
貝內特彗星 過近日點時彗尾已長達11度,亮度達0等。 後發現
於黎明 前的東方天空,彗尾日漸變長,達20度以上,粗而彎的橙黃色
塵埃彗尾 和直線延伸的藍色氣體彗尾漂亮而易於區分。它成為自1910年
哈雷彗星 回歸以來最輝煌的彗星之一,很多天文愛好者都拍到頗為漂亮的照片。
貝內特彗星是1969年12月28日由
南非 業餘天文學家
貝內特 發現而命名的。
哈雷彗星
哈雷彗星是惟一可以預報的
大彗星 ,1705年,英國天文學家
哈雷 利用牛頓
萬有引力定律 推算出其回歸周期及軌道,為表彰他的成就,遂將該彗星命名為哈雷。它成為公元前240年以來有32次回歸記錄的“熟客”。
哈雷彗星 的周期約為76年。在20世紀有二次出現。1910年回歸時條件良好,因而形象頗為壯觀:4月20日過近日點時
彗尾 已亮得肉眼可見,一個月後過近地點時彗尾長達125度~150度。其時,由於它距離地球只有2500萬千米,故有人擔心完全被彗尾籠罩的地球生物會全部死亡。其實彗尾非常稀薄,而地球未發生任何異狀。不過哈雷彗星橫掃天際的景象著實使當時的人們心驚肉跳。
天象 2002年3月5日13:15由中國河南省開封市天文愛好者張大慶和日本業餘天文學家遲谷熏在上月初共同發現的“池谷—張彗星”,日前天文學家已計算出其軌道,它將在3月18日通過近日點,這將為國內的眾多天文愛好者提供一次觀測新彗星的良機。據介紹,“池谷—張彗星”已逐漸靠近近日點,此後十餘天的每天黑幕降臨時分,該彗星會在西南方天空出現,
地平高度 約在20°左右,可用口徑為5厘米左右的小型天文望遠鏡觀測。特別是從3月15-20日的數天時間,這顆彗星的亮度還將繼續增亮,其亮度估計在4星等左右,在無燈光干擾、大氣 寧靜度較高的郊外用肉眼可看到一顆像蒲公英狀的模糊亮點,即“池谷—張彗星”
近日點和遠日點太陽輻射  近日點相關公式計算
近日點相關公式計算 近日點經度分布
近日點經度分布 近日點和遠日點太陽輻射
近日點和遠日點太陽輻射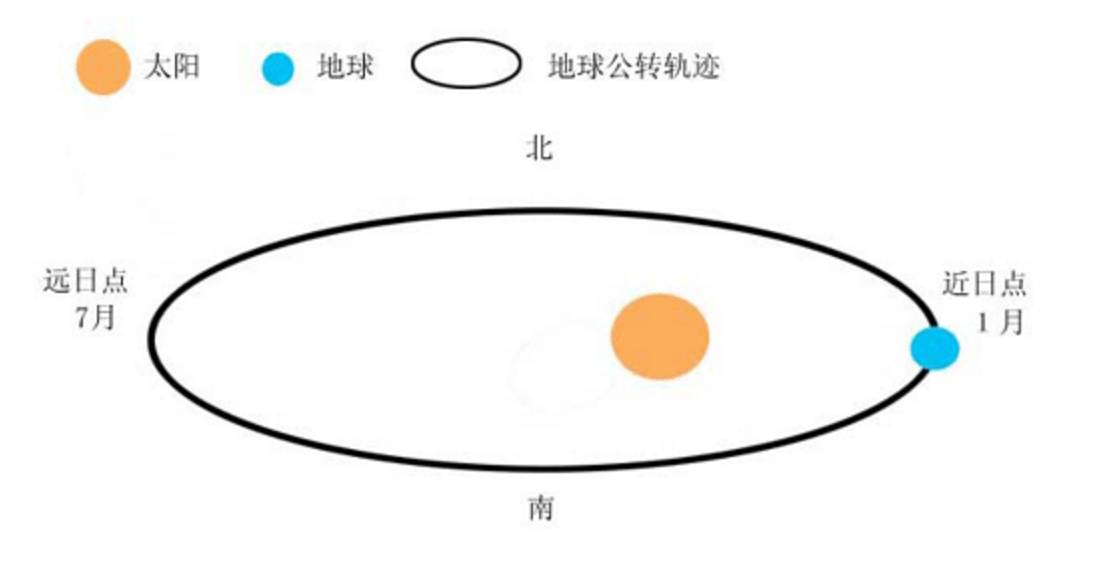
 近日點相關公式計算
近日點相關公式計算 近日點經度分布
近日點經度分布 近日點和遠日點太陽輻射
近日點和遠日點太陽輻射