基本介紹
學科介紹,分支體系,歷史起源,研究對象,研究方法,研究成果,哈雷與彗星,測量地球,測量太陽視差,恆星物理學,月球空間探測,行星衛星探測,天體力學,天體測距方法,雷達遙測,恆星視差法,光譜視差法,變星,超新星,Tulley-Fisher,哈勃定律,其他測距方法,實例,
學科介紹
天體測量依觀測所用的技術方法和發展順序，可以分為基本的、照相的、射電的和空間的四種。把已經精確測定位置的天體作為天球上各個區域的標記，選定坐標軸的指向，就可以在天球上確定一個基本參考坐標系，用它來研究天體（包括地球和人造天體）在空間的位置和運動。這種參考坐標系，通常用基本星表或綜合星表來體現。
分支體系
天文地球動力學
歷史起源
天體測量學的起源可以追溯到人類文化的萌芽時代。遠古時候為了指示方向、確定時間和季節，先後創造出日晷和圭表。對茫茫星空的觀測，導致劃分星座和編制星表，進而研究太陽、月球和各大行星在天球上的運動。當時的天體測量學既奠定了曆法的基礎，又確認了地球的自轉和公轉在天球上的反映，從而逐漸形成古代的宇宙觀。因此，早期天文學的主要內容就是天體測量學。
天體坐標系
天體坐標系根據浩瀚的天體測量資料，經過精心研究得出的克卜勒行星運動三大定律，為天體力學的建立創造了重要條件。天體力學與天體測量學一向是密切配合的，依靠觀測太陽、月球、大行星和小行星的大量資料和天體力學的研究方法，總結出太陽系天體（特別是地球和月球）的運動理論。它不但為太陽系演化的研究提供素材，而且是測定天文時間與導航工作的重要依據。
研究對象
對恆星的位置、自行和視差觀測所得到的恆星的空間分布和運動狀態的資料，是研究天體物理學，特別是研究恆星天文所需的基本資料。對銀河繫結構、星團和星協動力學演化、雙星系統和特殊恆星的研究及宇宙學的研究，都需要依據大量的天體測量資料，這就對天體測量學提出更高的要求。
目前的天體制量的手段，已從可見光觀測發展到射電波段，以及紅外、紫外、X射線和γ射線等波段的觀測；在觀測方式上，已由測角擴展到測距；觀測所在地已由固定天文台發展為流動站、全球性組網觀測以及空間觀測；觀測精度正在走向千分之一角秒和厘米級觀測的天體也向星數更多、星等更暗的光學恆星、星系射電源和紅外源等擴展。
可以預期，現代的天體測量學不但能以厘米級的精度完成實用天文學的任務，建立更理想的基本參考坐標系，進一步推動天文地球動力學的研究，而且還能提供十分豐富的基礎資料，為天體物理學、天體演化學和宇宙學的新理論開闢道路。
研究方法
通過研究天體投影在天球上的坐標，在天球上確定一個基本參考坐標系，來測定天體的位置和運動，這種參考坐標系，就是星表。在實際套用中，可用於大地測量、地面定位和導航。地球自轉和地殼運動，會使天球上和地球上的坐標系發生變化。為了修正這些變化，建立了時間和極移服務，進而研究天體測量學和地學的相互影響。古代的天體測量手段比較落後，只能憑肉眼觀測，對於天體測量的範圍有限。隨著時代的發展，發現了紅外線、紫外線、X射線和γ射線等波段，天體測量範圍從可見光觀測發展到肉眼不可見的領域，可以觀測到數量更多的、亮度更暗的恆星、星系、射電源和紅外源。隨著各種精密測量儀器的出現，測量的精度也逐漸提高。
天體測量學內容在天文學產生後的一段很長時間裡，人類只限於用肉眼觀測太陽、月亮、行星和恆星在天空中的位置，研究它們的位置隨時間變化的規律。在對星星測量的基礎上，古代的天文學家注意到恆星在天空的位置相對不動，由此繪製出星圖，劃分星座和編制星表；進而研究太陽、月亮及行星的運動，在測量天體視運動的基礎上編制曆法。
17世紀初發明了望遠鏡；17世紀下半葉又創立了微積分，發現了萬有引力定律。擁有望遠鏡的巴黎天文台和格林尼治天文台相繼建立起來了。天體測量學的新發現，如光行差現象、地軸的章動現象、恆星視差的測定等等接連為人們所認識，天體測量學的成果通過時間服務和曆書編算（即授時和編歷）等，被運用到大地測量和航海事業等方面。
研究成果
為紀念這一學科的重要性，小行星25000被稱為“天體測量”（Astrometria）。為了航海的需要，法國首先於1671年設立了巴黎天文台，英國也不甘落後，於1675年設立了格林威治皇家天文台。後來俄國的普爾科沃天文台、美國的華盛頓海軍天文台也相繼建成。而這個時期從事天體測量工作的主要是以天文台為基地的專業天文工作者。
哈雷與彗星
在航海天文學上發揮最大作用的是英國格林威治天文台，它的第二任台長是哈雷，21歲那年他毅然放棄獲得學位的良機，決心去測量南天星辰的位置。在父親的支持下，攜帶觀測儀器，來到南大西洋，建立了一座臨時天文台，一年之內便作成了第一個南天星辰表，這使他在22歲時便享有盛名，稱他為“南天的第谷”。他與牛頓一見如故，致力於彗星軌道的研究，套用萬有引力定律，把所有能找到充分觀測資料的彗星軌道一一推算出來。他發現1531年、1607年和1682年3次觀測的彗星軌道十分相似，而且預言這顆彗星將在1758年和1759年再次歸來，它果然如期而來，但哈雷已於1742年去世，為了紀念他的功績，人們把這顆彗星命名為“哈雷彗星”。
古代觀測天體
古代觀測天體測量地球
由於人們承認日心體系，又因天體距離測量的需要，人們迫切想知道地球的大小。18世紀以來，人們又努力去探討地球的扁平形狀問題。牛頓曾從理論上推測，地球的形狀是兩極較扁而赤道部分突出。牛頓的看法遭到了法國學者的反對，經測量巴黎天文台認為地球是西瓜形的。爭論從17世紀末開始，一直延續了半個世紀之久。
測量太陽視差
地球到太陽的距離通常是用太陽的地心視差來表示。地心視差指的是地球半徑對天體的張角。知道了這個角，有知道了地球半徑的長度，地球到某一天體的距離就很容易求出了。但困難的是太陽距離地球很遠，直接測量地心差誤差很大，於是天文學家轉而去求行星的視差。
恆星物理學
19世紀恆星測量學已經發展得相當完善，可以很精確地測定出恆星的方位，到19世紀末，運用三角視差求出距離的恆星已經多達七十餘顆。19世紀中葉在太陽物理學的刺激下，恆星物理學發展起來，促使天文學家使用分光鏡研究恆星。義大利教授賽奇把恆星按照光譜分成4類，即白星、黃星、橙紅星、深紅星，賽奇認識到這樣的分類是和恆星的溫度有關的；英國的哈斯根弄清了這些恆星的化學組成，指出亮星具有和太陽相同的化學組成，它們的光線來自下層熾熱物，穿過高層具有吸收能力的大氣層而向外輻射。
日趨成熟的太陽光譜研究，相當於把地球上的動植物種屬進行了仔細的分類，19世紀後期光譜工作的結果以更精細更有意義的方式，將恆星按光譜型分了組，從而使天文學家們產生了恆星演化的想法，這一想法在20世紀結出了豐碩的成果。
月球空間探測
1957年人類進入太空時代以後，對太陽系的研究發生了根本的變化，對月球進行多學科的研究。1961年美國“阿波羅”計畫開始，先後執行“徘徊者”、“月球勘測者”、“月球軌道飛行器”三個輔助計畫，1966年正式實施“阿波羅”登月計畫，1972年結束。1969年7月20日“阿波羅”實現了第一次人類登月的創舉。對月球進行了觀測、照相、採樣，還在月面上安裝了各種實驗儀器，發射了月球衛星。
牛頓手制的反射望遠鏡
牛頓手制的反射望遠鏡“阿波羅”飛行獲得了大量關於月球的科學資料，詳盡地揭示了月球表面的結構特徵，月面物質的化學成分、光學和熱學的物理特性，並探測了月球的重力、磁場和月震等。前蘇聯的“月球號”探月計畫，首次拍得月球背面照片，據此天文學家繪製了世界第一張月背圖。
該計畫的實施，使月球有了自動科學站，由地面站操縱，在月球上自動執行考察任務。對月球的太空探測，使人類對它的認識進入了嶄新階段，對月球的深層研究開始。
行星衛星探測
人類關注的第二顆行星是火星。這顆紅色的星球自古以來就對天文學家有一種誘惑力，它是我們地球的鄰居。1964年美國“水手4號”拍攝了火星照片，發現了火星表面有不少像月球上那樣的環行山，1971年發現火星上有巨大的火山、峽谷和寬敞的河床，還特別做了生物探測實驗，結果表明火星上不存在生命。美、蘇兩國的探測活動揭開了金星表面的神秘面紗，原來金星表面被一層濃密的大氣包圍，大氣中的二氧化碳含量占97%以上，產生極為強烈的溫室效應，致使其表面溫度高達465~485℃，而且基本上沒有地區、季節、晝夜的區別。金星表面大氣層頂部存在著與其自轉方向相同、速度高達320千米/秒的大環流。金星表面的大氣壓約為地球的90倍，而且有非常頻繁的放電現象。金星表面被濃雲密霧所覆蓋，用普通攝影的方法無法了解其表面真實情況，美國科學家用雷達手段，對金星表面93%的地形進行勘察，繪出了精密的金星表面圖，金星的表面被名為玄武岩的火成岩覆蓋著。
截止21世紀，只有一艘探測器探測過水星，美國“水手10號”曾3次飛臨水星，對水星表面60%的區域做了攝影考察，得到大量水星情報。水星的表面很像月球，有大大小小的環形山，其表面大氣一直非常稀薄，晝夜溫差十分懸殊。“水手10號”還發現水星有磁場，與地球磁場相似，是偶極場。
木星和土星是各種媒體和人們關注最多的話題，是行星探測器光顧最多的兩顆行星，發回了大量照片，獲得重大發現，包括木星環、極光、木衛一的火山爆發和關於5顆木衛的精彩照片，證實了木星的磁層、磁場、輻射帶和極光。
天體力學
天所謂經典天文學是指天體測量學和天體力學。天體測量學主要是研究和測量天體的位置和運動的，它是天文學中最先發展起來的一個分支，可以說，早期天文學的內容就是天體測量學。天體力學是研究天體運動和形狀的科學，它是在天體測量學的基礎上發展起來的。克卜勒提出的行星運動三定律，為天體力學的建立創造了條件。牛頓提出的萬有引力定律則奠定了天體力學的基礎。18世紀天文學的主流是為了制定曆法和航海的需要而進行的精密的子午線觀測、月球運動的觀測和日地距離的測定等，所以天體測量學占主導地位。但在18世紀末，天體力學取得了與天體測量學並肩的地位。
火星極地著陸者”探測器天體力學與天體測量學一向是密切配合的，依靠觀測太陽、月球、大行星和小行星的大量資料和天體力學的研究方法，總結出太陽系天體（特別是地球和月球）的運動理論。它不但為太陽系演化的研究提供素材，而且是測定天文時間與導航工作的重要依據。在航天時代，天體測量技術的提高與天體力學方法的改進，更是相輔相成，互相推動。例如，研究人造衛星和宇宙飛行器的軌道，研究地球和月球運動的細節，都需要天體力學與天體測量學的配合。
對恆星的位置、自行和視差觀測所得到的恆星的空間分布和運動狀態的資料，是研究天體物理學，特別是研究恆星天文所需的基本資料。對銀河繫結構、星團和星協動力學演化、雙星系統和特殊恆星的研究及宇宙學的研究，都需要依據大量的天體測量資料，這就對天體測量學提出更高的要求。
隨著科學技術的發展，探空火箭、人造衛星和探測器的相繼發射，突破了地球大氣與磁場這兩道屏障，賦於天文學以嶄新的生命力。氣象衛星、測量衛星、地球資源衛星等等從環繞地球的軌道上，居高臨下仔細觀測地球，使我們對地球的認識大大前進了一步。千百年來，我們對太陽系中的其他天體只能從遠處憑跳，可望而不可及。現在，我們既能發射探測月球和各行星的衛星，並已把探測器降落到幾個行星表面，直接收集第一手材料。隨著觀測設備和手段的不斷進步，觀測的波段也由單一的光學觀測發展到全波段觀測，使X射線天文學、γ射線天文學、紅外天文學和紫外天文學等新的研究領域爭放異彩。在空間技術高度發展的21世紀，天文觀測研究已由地面觀測進入空間時代。
天體測距方法
測量宇宙的距離好像爬樓梯一樣，從近距離到遠距離一層一層的往上爬。而測量的距離的方法也好像接力賽跑者一樣，各扮演著不同先後的角色，合力完成測量宇宙距離的任務。
銀河系內測距
銀河系內測距距離指標需要用前一階指標來校準，自然地，不準確也逐漸累積，所以對愈大距離的天體，距離的不確定愈高。
天文學家用來作為遠距離指標的天體計有：新星、發射星雲、行星狀星雲、球狀星團、I 型超新星、星系…...其中，行星狀星雲與I 型超新星的亮度範圍明確，亮度高，是較成功的遠距離指標。
遠距離指標經常需要利用近距離指標來校準，各種量距離方式的關聯性，可以用一倒立的“距離金字塔圖（the distance pyramid）” 來表示。
雷達遙測
（radar ranging)
1 AU = 149,597,870 公里≒1.5* 10^8 公里
測距適用範圍：～1AU。
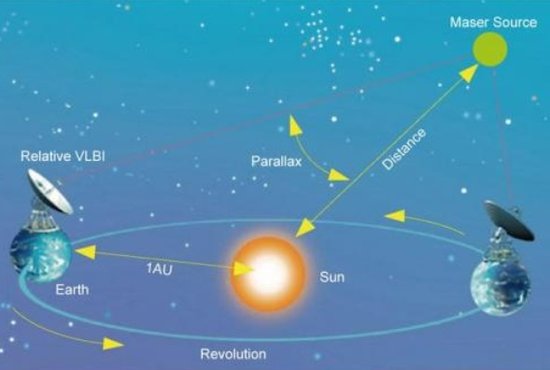
恆星視差法
（stellar parallax)
d （秒差距，pc) = 1/ p （視差角，秒弧）
1 pc 定義為造成一秒視差角的距離，等於3.26 光年。地面觀測受大氣視寧度的限制，有效的觀測距離約為100 pc （～300 光年）。在地球大氣層外的Hipparcos 衛星與哈勃望遠鏡，能用視差法量測更遠的恆星，範圍可推廣到1000 pc。
測距適用範圍：～1,000 pc。
光譜視差法
（spectroscopic parallax)
如果星體的視星等為mV，絕對星等MV，而以秒差距為單位的星體距離是d。它們間的關係稱為距離模數，公式為：
mV - MV = -5 + 5lgd
如果知道恆星的光譜分類與光度分類 ，由赫羅圖 可以找出恆星的光度。更進一步，可以算出或由赫羅圖讀出恆星的絕對星等，代入距離模數公式，即可以找出恆星的距離。
因為主序星的分布較集中在帶狀區域，所以光譜視差法常用主序星為標的。利用鄰近的恆星，校準光譜視差法的量測。另也假設遠處的恆星的組成與各項性質，大致與鄰近恆星類似。誤差常在25% 以上。（註：本銀河系直徑約30 Kpc)
測距適用範圍：～7Mpc。
例：若某恆星的視星等為+15 ，其光譜判定為G2 V 的恆星‘i從赫羅圖讀出該星的絕對星等為+5 ，代入距離模數公式15 - 5 = 5 log d - 5 ，求出該星的距離d= 1000 pc = 3260 光年。
變星
測定變星的光譜類別後，由周光圖可以直接讀出它的光度（絕對星等）。由變星的視星等和絕對星，利用距離模數公式，
mV - MV = -5 + log10d
即可定出變星的距離。目前發現，最遠的造父變星 在M 100，距離我們約17 Mpc。
測距適用範圍：～17 Mpc。
超新星
平均每年可以觀測到數十顆外星系的超新星。大部份的超新星（I 型與Ⅱ 型） 的最大亮度多很相近，天文學家常假設它們一樣，並以它們做為大距離的指標。
以造父變星校準超新星的距離，以找出I 型與Ⅱ 型星分別的平均最大亮度。由超新星的光度曲線 ，可以決定它的歸類。對新發現的超新星，把最大視亮度（mV) 與理論最大絕對亮度（MV) 帶入距離模數公式，即可找出超新星的距離。
Ⅱ 型超新星受外層物質的干擾，平均亮度的不確定性較高，I 型超新星較適合做為距離指標。
測距適用範圍：> 1000 Mpc。
Tulley-Fisher
漩渦星系的氫21 公分線，因星系自轉而有杜卜勒加寬。由譜線加寬的程度，可以找出譜線的位移量Δλ，並求出星系的漩渦臂在視線方向的速度Vr，公式為：
Δλ/λo = Vr/c = Vsin i/c
i 為觀測者視線與星系盤面法線的夾，由此可以推出漩渦星系的旋轉速率。Tulley 與Fisher 發現，漩渦星系的光度與自轉速率成正比，現在稱為Tulley-Fisher 關係。
量漩渦星系的旋轉速率，可以知道漩渦星系的光度，用距離模數公式，就可以找出漩渦星系的距離。Tulley-Fisher 關係找出的距離，大致與I 型超新星同級，可互為對照。
註：現常觀測紅外線區譜線，以避免吸收。
測距適用範圍：> 100 Mpc。
哈勃定律
幾乎所有星系相對於本銀河系都是遠離的，其遠離的徑向速度可用都卜勒效應來測量星系的紅位移 ，進而找出星系遠離的速度。
1929年Edwin Hubble得到遠離徑向速度與星系距離的關係如下：
哈勃定律：Vr = H*d
其中Vr = 星系的徑向遠離速度；H = 哈勃常數=87 km/(sec*Mpc)；d = 星系與地球的距離以Mpc 為單位。
哈柏定律是一個很重要的距離指標，量得星系的遠離速度，透過哈柏定律可以知道星系的距離。
例：室女群（Vigro cluster) 的徑向遠離速度為 Vr =1180 km/sec， 室女群與地球的距離為 d = Vr/H = 1180/70 = 16.8 Mpc。
測距適用範圍：宇宙邊緣。
其他測距方法
紅超巨星
假設各星系最亮的紅超巨星絕對亮度都是MV = -8 ，受解析極限的限制，適用範圍與光譜視差法相同。測距適用範圍：～7Mpc。
新星
假設各星系最亮的新星，絕對亮度都是MV = -8。測距適用範圍：～20 Mpc。
HⅡ 區
假設其他星系最亮的HⅡ區之大小，和本銀河系相當。（定H Ⅱ區的邊界困難，不準度很高）
假設星系行星狀星雲，光度分布的峰值在MV = - 4.48。測距適用範圍：～30 Mpc。
球狀星團
假設星系周圍的球狀星團，光度分布的峰值在MV = - 6.5。測距適用範圍：～50 Mpc。
Faber-Jackson 關係、D-σ關係
Faber-Jackson 關係與Tulley-Fisher 關係類似，適用於橢圓星系。Faber-Jackson 關係：橢圓星系邊緣速率分布寬度σ的四次方與星系的光度成正比。
D-σ關係：橢圓星系邊緣速率分布寬度σ與星系的大小D 成正比。測距適用範圍：> 100 Mpc。
星系
假設其他更遠的星系團，與室女星系團中最亮的星系都具有相同的光度MV = -22.83。測距適用範圍：～4,000 Mpc。
實例
室女座星系團的距離
本超星系團(Local Supercluster) 含本星系群，大熊座星系群，室女座星系團 和其他星系群。下表為用數種測距方法量得的室女座星系團的距離，測宇宙距離常需要比對不同方法所定出的距離，室女座星系團的距離平均值約為16 Mpc。
方法 | 室女座星系團的距離 (Mpc) | 適用範圍（Mpc) |
造父變星 | 14.9 ±1.2 | 20 |
新星 | 21.1 ±3.9 | 20 |
行星狀星雲 | 15.4 ±1.1 | 30 |
球狀星團 | 18.8 ±3.8 | 50 |
Tulley-Fisher關係 | 15.8 ±1.5 | > 100 |
D-σ關係 | 16.8 ±2.4 | > 100 |
I 型超新星 | 19.4 ±5.0 | > 1000 |
