天體的運動軌跡為圓錐曲線(橢圓、拋物線和雙曲線),其中橢圓曲線軌道為克卜勒軌道,逃逸拋物線和雙曲線軌道為非克卜勒軌道。非克卜勒軌道可以分為單心引力場和多心引力場。
基本介紹
- 中文名:克卜勒軌道
- 外文名:Keplerian orbits
- 簡介:天體的運動軌跡之一
- 特徵:橢圓曲線軌道
- 運動軌跡分類:圓錐曲線:橢圓、拋物線和雙曲線
簡介,克卜勒軌道,克卜勒軌道來源,定義,分類和特點,
簡介
人類科學認識天體運動是從哥白尼(1473—1543)開始的,克卜勒(1571—1630)根據前人的天文觀測資料總結出了行星繞太陽運動的三大定律,被後人稱為克卜勒三定律。克卜勒和伽利略(1564—1642)之後,牛頓(1642—1727)提出了萬有引力定律和物體運動的三大定律(後人稱之為牛頓三定律),以此為基礎的牛頓力學是天體力學的基礎,也是航天動力學的基礎。克卜勒定律給出了行星(也適用於太空飛行器)軌道運動規律的運動學描述,牛頓力學則是對這種軌道運動規律給出了動力學意義下的解釋。克卜勒定律可以用牛頓力學得到嚴格證明。從哥白尼的日心地動說的提出到牛頓力學的建立是人類認識宇宙的第一次飛躍。
二體問題是天體力學中的一個基本問題,它是指可視為質點的兩個天體在相互間唯一的萬有引力作用下的運動規律問題。二體問題可以用牛頓萬有引力定律和牛頓運動定律來描述並得到完全解決。克卜勒三定律是二體問題的解。在二體問題的假設條件下,進一步假設主天體的質量遠遠大於次天體(或太空飛行器)的質量,且認為主天體是慣性固定的,就成了限制性二體問題。
太空飛行器軌道是指太空飛行器在天體引力和其它外力作用下其質心運動的軌跡。由於受到天體中心引力以外的其它外力的作用,太空飛行器的軌道運動實際上並不嚴格遵循二體問題的解,這發生在太空飛行器受到地球非球形及質量分布不均勻、大氣阻力、太陽光壓、其它天體的引力等自然環境攝動力作用的情況,也發生在太空飛行器受到其主動產生的控制力作用的情況。這些情況下太空飛行器的軌道不再是嚴格的有時甚至根本不是理想的克卜勒軌道了,於是提出了非克卜勒軌道問題。從軌道動力學和軌道控制的角度可以把太空飛行器軌道分為克卜勒軌道(KO)和非克卜勒軌道(NKO),太空飛行器克卜勒軌道分為理想KO和視同KO兩大類,太空飛行器非克卜勒軌道分為非本質NKO和本質NKO兩大類,這兩類NKO中又有自然(被動)的和人為(主動)的兩種情況。
克卜勒軌道
克卜勒軌道來源
作為一個名詞術語,克卜勒軌道來自克卜勒三定律,起源於對行星繞太陽的運動規律———行星軌道問題的研究。“克卜勒軌道”這個名詞是克卜勒以後的人提出來的,並把克卜勒軌道擴展到二體問題的解。克卜勒軌道的英文名詞是Keplerian orbits,本文把它縮寫為KO。由於太空飛行器的軌道運動也符合克卜勒三定律,因此名詞“克卜勒軌道”同樣適用於太空飛行器。本文所說克卜勒軌道大多數情況是指太空飛行器克卜勒軌道。
定義
克卜勒軌道定義包括:
- 符合克卜勒三定律的天體或太空飛行器的運行軌道。
- 由二體問題的解得到的天體或太空飛行器的運行軌道。
所以,克卜勒軌道也稱為二體問題軌道。符合上述定義的克卜勒軌道也稱為理想的克卜勒軌道。
分類和特點
克卜勒軌道的分類見圖。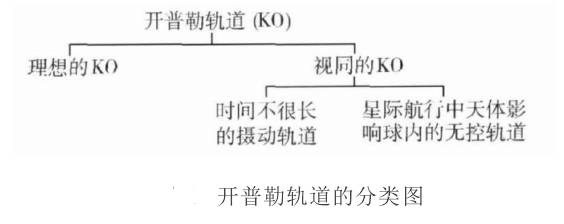

圖中的“視同”是“可以把它看作”的意思。視同KO的特點如圖所示。太空飛行器的克卜勒軌道可由如下二體問題基本方程解得:

上述方程描述在慣性坐標系中太空飛行器相對於天體的軌道運動。式中的r是從天體(質量記為m1)到太空飛行器(m2)的位置矢量,μ=G(m1+m2)是二體系統的引力常數,G是萬有引力常數。由於m1>>m2,可以只考慮m1對m2的引力,這種情況可把太空飛行器克卜勒軌道看成是限制性二體問題的解,即看成是在慣性固定天體中心引力場中的運動(有心力運動)軌跡。
由上式可以解得太空飛行器的軌道方程