簡介 “誰不知道熵概念就不能被認為是科學上的文化人,將來誰不知道分形概念,也不能稱為有知識。”——物理學家
惠勒 分形理論 是在上世紀70年代由芒德布羅幾乎集一己之力創立的,但其嚴格的
數學基礎 之一——
芒德布羅集 ,卻是70年代末芒德布羅及布魯克斯、馬蒂爾斯基以及道阿迪、哈伯德、沙斯頓等人幾乎同時分別建立完善的,他們的思想都源自上世紀
前葉 一些前輩如法圖、
萊維 、朱利亞的有關思想。
耶魯大學網站Benoît B. Mandelbrot個人主頁
中文文獻中芒德布羅的譯名一直不統一,芒德布羅本人使用的中文名字是“
本華·曼德博 ”,可見於其
耶魯大學 網站
個人主頁 照片,為
豎排 繁體漢字
手寫體 。
全國科學技術名詞審定委員會 在數學、物理學、力學等幾個學科術語的譯名中,使用的都是“芒德布羅”。本華·曼德博(1924-2010,法語原文Benoît B. Mandelbrot),生於
波蘭 的
立陶宛 裔
猶太 家庭,主要
成長教育 經歷是在法國完成的,後長期在美國工作。如果追求音譯的準確,還應考慮Mandelbrot姓氏最初的來源,這是一個明顯地具有阿什肯那茲猶太姓氏特徵的姓(德語“杏仁”+“麵包”)。
分形現已成為套用極為廣泛的學科。芒德布羅
個人風格 獨特,對各類看似“
無定形 ”、“不光滑”的“怪東西”皆富有興趣,也正是這樣他才能最終抽象創立出分形這門學科。曼德布羅特來訪過中國大陸一次以上,稱中國文字個個是圖形,與他路數相合(芒德布羅本人習用法語)。中國最早使用分形理論的可能是金屬學界。
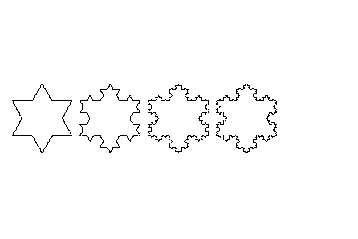
現今人們熟悉的分形的著名實例,如用“鏤空”辦法製成的
康托爾集 、
謝爾賓斯基三角形 (Waclaw Sierpinski,1882-1969,波蘭數學家)及門格
乳酪 或稱
門格海綿 (Menger,1902-1985,為著名經濟學家門格之子),它們的非整數
維數 是漸增的,分別為0.63、1.58、2.72,而它們長度、面積、體積令人吃驚的皆為0。另一個用“凸起”辦法製作的
科赫曲線 (H.von Koch,1870-1924,
瑞典 數學家),其維數是1.26,它的長度則是無限的,可它圍住的面積卻有限。
分形作為一種
數學工具 ,現已套用於各個領域,如套用於計算機輔助使用的各種分析軟體中。
由來 據芒德布羅教授自己說,fractal一詞是1975年夏天的一個寂靜夜晚,他在冥思苦想之餘偶翻他兒子的
拉丁文 字典時,突然想到的。此詞源於拉丁文形容詞
fractus ,對應的拉丁文動詞是frangere(“破碎”、“產生無規碎片”)。此外與英文的fraction(“碎片”、“分數”)及fragment(“碎片”)具有相同的詞根。在70年代中期以前,芒德布羅一直使用英文
fractional 一詞來表示他的分形思想。因此,取拉丁詞之頭,擷英文之尾的fractal,本意是不規則的、破碎的、分數的。芒德布羅是想用此詞來描述自然界中傳統歐幾里德幾何學所不能描述的一大類複雜無規的幾何對象。例如,彎彎曲曲的海岸線、起伏不平的山脈,粗糙不堪的斷面,變幻無常的浮雲,九曲迴腸的河流,縱橫交錯的血管,令人眼花繚亂的滿天繁星等。它們的特點都是,極不規則或極不光滑。直觀而粗略地說,這些對象都是分形。
探討 幾何學 分形幾何與傳統幾何相比有什麼特點:
⑴從整體上看,分形幾何圖形是處處不規則的。例如,海岸線和山川形狀,從遠距離觀察,其形狀是極不規則的。
⑵在不同尺度上,圖形的
規則性 又是相同的。上述的海岸線和山川形狀,從近距離觀察,其局部形狀又和整體形態相似,它們從整體到局部,都是自相似的。當然,也有一些分形幾何圖形,它們並不完全是自相似的。其中一些是用來描述一般
隨機現象 的,還有一些是用來描述混沌和
非線性系統 的。
什麼是分維 在
歐氏空間 中,人們習慣把空間看成三維的,平面看成二維,而把直線或曲線看成一維。也可以稍加推廣,認為點是
零維 的,還可以引入
高維空間 ,但通常人們習慣於整數的維數。
分形理論 把維數視為分數,這類維數是物理學家在研究混沌
吸引子 等理論時需要引入的重要概念。為了定量地描述
客觀事物 的“非規則”程度,1919年,數學家從測度的角度引入了維數概念,將維數從整數擴大到分數,從而突破了一般拓撲集維數為整數的界限。
分維的概念可以從兩方面建立起來:一方面,首先畫一個線段、
正方形 和
立方體 ,它們的邊長都是1。將它們的邊長
二等分 ,此時,原圖的
線度 縮小為原來的1/2,而將原圖等分為若干個相似的圖形。其線段、正方形、立方體分別被等分為2^1、2^2和2^3個相似的子圖形,其中的指數1、2、3,正好等於與圖形相應的經驗維數。一般說來,如果某圖形是由把原圖縮小為1/a的相似的b個圖形所組成,有:
a^D=b,D=(ln b)/(ln a)
的關係成立,則指數D稱為
相似性 維數,D可以是整數,也可以是分數。另一方面,當畫一根直線,如果用0維的點來量它,其結果為無窮大,因為直線中包含無窮多個點;如果用一塊平面來量它,其結果是0,因為直線中不包含平面。只有用與其同維數的小線段來量它才會得到有限值,而這裡直線的維數為1(大於0、小於2)。與此類似,如果畫一個
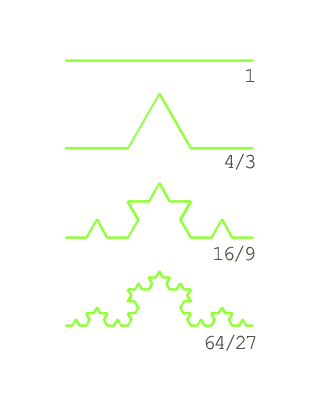
Koch曲線 ,其整體是一條無限長的線摺疊而成,顯然,用小直線段量,其結果是無窮大,而用平面量,其結果是0(此曲線中不包含平面),那么只有找一個與Koch曲線維數相同的
尺子 量它才會得到有限值,而這個維數顯然大於1、小於2,那么只能是小數(即分數)了,所以存在分維。
Koch曲線 的每一部分都由4個跟它自身比例為1:3的
由若干條Koch曲線組成的Koch雪花
形狀相同的小曲線組成,那么它的
豪斯多夫維數 (分維數)為d=log(4)/log(3)=1.26185950714...
概況 定義 芒德布羅曾經為分形下過兩個定義:
(1)滿足下式條件
Dim(A)>dim(A)
的集合A,稱為分形集。其中,Dim(A)為集合A的Hausdoff
維數 (或
分維數 ),dim(A)為其
拓撲維數 。一般說來,Dim(A)不是整數,而是分數。
然而,經過理論和套用的檢驗,人們發現這兩個定義很難包括分形如此豐富的內容。實際上,對於什麼是分形,到當下為止還不能給出一個確切的定義,正如生物學中對“生命”也沒有嚴格明確的定義一樣,人們通常是列出
生命體 的一系列特性來加以說明。對分形的定義也可同樣的處理。
分形一般有以下特質:
(i)分形集都具有任意
小尺度 下的比例細節,或者說它具有精細的結構。
(ii)分形集不能用傳統的幾何語言來描述,它既不是滿足某些條件的點的
軌跡 ,也不是某些簡單方程的解集。
(iii)分形集具有某種自相似形式,可能是近似的自相似或者統計的自相似。
(iv)一般,分形集的“
分形維數 ”,嚴格大於它相應的拓撲維數。
(v)在大多數令人感興趣的情形下,分形集由非常簡單的方法定義,可能以變換的疊代產生。
意義 上世紀80年代初開始的“分形熱”經久不息。分形作為一種新的概念和方法,正在許多領域開展套用探索。美國物理學大師
約翰·惠勒 說過:今後誰不熟悉分形,誰就不能被稱為科學上的文化人。由此可見分形的重要性。
中國著名學者
周海中 教授認為:
分形幾何 不僅展示了數學之美,也揭示了世界的本質,還改變了人們理解自然奧秘的方式;可以說分形幾何是真正描述大自然的
幾何學 ,對它的研究也極大地拓展了人類的認知疆域。
分形幾何學 作為當今世界十分風靡和活躍的
新理論 、新學科,它的出現,使人們重新審視這個世界:世界是非線性的,分形無處不在。分形幾何學不僅讓人們感悟到科學與藝術的融合,數學與
藝術審美 的統一,而且還有其深刻的
科學方法論 意義。
歷史背景 在傳統的幾何學中,人們研究一個幾何對象,總是習慣於在
歐幾里得空間 (Rn,Euclidean)對其研究和度量,其中字母n
表示空間 的維數,通常為整數,如n分別為1、2、3時,對應的空間為
線性空間 、平面空間、立體空間,在相應的空間中,可以測得幾何對象的長度、面積、體積等。但是大約在1個世紀前,在數學領域,相繼出現了一些被稱為數學怪物(mathematical monsters)的東西,在傳統的Euclid領域,人們無法用幾何語言去表述其整體或
局部性質 ,其中,比較著名的
數學怪物包括:
Von Koch曲線
科赫曲線 此曲線在一維下測量任意段長度為
無窮大 (想像中,考慮到能測量原子的維度);在二維下測量面積為零
這些數學怪物困擾數學家許多年,直至20世紀,被美國數學家Benoit B. Mandelbrot創立的
分形幾何學 (fractal geometry)徹底解決。Mandelbrot提出:之所以無法用幾何語言去描述這些數學怪物,是因為在維數為整數的空間中,用維數同樣是整數的“
尺子 ”對其丈量、描述;而維數不應該僅僅是整數,可以是任何一個
正實數 ;只有在幾何對象對應的維數空間中,才能對該
幾何體 進行合理的整體或局部描述。以上圖的
Koch曲線 為例,其維數約為1.26,套用同樣為1.26維的尺子對其進行描述,比如取該曲線前1/4段作為單位為1的尺子去丈量這個幾何體,此幾何體長度為4。也正是因其維數介於1維與2維之間,所以此幾何體在1維下長度為無窮大,2維下面積為零。
Fractal這個詞是由Mandelbrot於1975創造的,來源於
拉丁文 “Fractus”,其英文意思是broken,即為“不規則、支離破碎”的物體。1967年,Mandelbrot在美國《Science》雜誌上發表題目為《英國的海岸線有多長》的劃時代論文,標誌著其分形思想萌芽的出現。1977年,Mandelbrot在
巴黎 出版的
法文 著作《Les objets fractals:forme,hasard et dimension》,1977年,在美國出版其英文版《Fractals:From,Chance,and Dimension》(《分形:形狀機遇和維數》),同年,他又出版了《The Fractal Geometry of Nature》(《大自然的分形幾何》),但是這三本書還未對社會和學術界造成太大的影響。直到1982年,《The Fractal Geometry of Nature》(《大自然的分形幾何》)第二版才得到
歐美 社會的廣泛關注,並迅速形成了“分形熱”,此書也被
分形學 界視為分形“聖經”。
發展史 1883年 Cantor集合被創造
1895年 Weierstrass曲線被創造,此曲線特點是“處處連續,點點不可微”
1919年 描述複雜幾何體的Hausdorff維問世
1951年 英國水文學家Hurst通過多年研究
尼羅河 ,總結出Hurst定律
1967年 Mandelbrot在《Science》雜誌上發表論文《英國的海岸線有多長》
1975年 Mandelbrot創造“Fractals”一詞
1975年 Mandelbrot在巴黎出版的
法文 著作《Les objets fractals:forme,hasard et dimension》
1977年 Mandelbrot在美國出版英文著作《Fractals:Form,Chance,and Dimension》以及《The Fractal Geometry of Nature》
1982年 《The Fractal Geometry of Nature》第二版,並引發“分形熱”
1991年 英國的Pergman出版社創辦《Chaos,Soliton and Fractal》雜誌
1998年 在
馬爾他 (Malta)的
瓦萊塔 (Valletta)召開了“分形98年會議”(5th International Multidisciplinary Conference)
2003年 在德國的Friedrichroda召開了“第三屆分形幾何和推測學國際會議”
2004年 在
加拿大 (Canada)的
溫哥華 (Vancouver)召開了“分形2004年會議”(8th International Multidisciplinary Conference)
種類 吸引子 :點在疊代的作用下得到的結構。一般可以用
微分方程 確立。例如:Lorenz吸引子。
套用 分形誕生在以多種概念和方法相互衝擊和融合為特徵的當代。分形混沌之旋風,橫掃數學、理化、生物、大氣、海洋以至社會學科,在音樂、美術間也產生了一定的影響。
分形所呈現的無窮玄機和美感引發人們去探索。即使不懂得其中深奧的數學哲理,也會為之感動。
分形使人們覺悟到科學與藝術的融合,數學與
藝術審美 上的統一,使從前枯燥的數學不再僅僅是抽象的哲理,而是具體的感受;不再僅僅是揭示一類存在,而是一種
藝術創作 ,分形搭起了科學與藝術的橋樑。
“分形藝術”與普通“電腦繪畫”不同。普通的“
電腦繪畫 ”概念是用電腦為工具從事美術創作,創作者要有很深的美術功底。而“分形藝術”是純數學產物,創作者要有很深的數學功底,此外還要有熟練的編程技能。
1、製作成各種尺寸的
裝飾畫 (用卡紙裝裱,可獲得很好的裝飾畫效果)。
2、用作包裝材料圖案,效果新穎。
4、套用於印染行業。
劉華傑博士認為:
1、將高精度
分形圖 形具體套用在建築設計中,可以考慮將
整面 牆壁用一幅分形圖裝飾。
2、研究分形
建築陶瓷 紋樣、分形紡織紋樣設計及其印染工藝。
3、設計分形時裝。
4、將分形圖形用於信息加密防偽。
軟體 Ultra Fractal
Visions of Chaos
Fraciant
Incendia
Mandelbulb 3D
Jwildfire
MathStudio(手機軟體)
案例 羅馬花椰菜 羅馬花椰菜 (RomanescoBroccoli)一小簇是整個花簇的一個分支,而在不同尺度下它們具有自相似的外形。換句話說,較小的分支通過放大適當的比例後可以得到一個與整體幾乎完全一致的花簇。因此可以說羅馬花椰菜花簇是一個分形的實例。
傳統醫學 最古老的樸素分形集(幾千年歷史,最簡單的分形集陰陽集),1999年,鄧宇等。
陰陽集,分維D=1
陰陽五行-臟腑(
藏象 :五臟五腑)的分維D=2.0959.