芒德布羅集(Mandelbrot set)是分形幾何和復動力學中一個非常有趣而又典型的集合:平方與加法是定義芒德布羅集所需要的程式開始,這實際上就是定義芒德布羅集所需要的一切。
基本介紹
- 中文名:芒德布羅集
- 外文名:Mandelbrot set
- 所屬學科:數學
- 所屬問題:動力系統(復動力系統)
- 相關概念:洗牌法,吉爾布雷思原理等
基本介紹,平方與加法,周期點,完整的芒德布羅集,芒德布羅集和茹利亞集,
基本介紹
對於二次多項式 ,芒德布羅集M定義為
,芒德布羅集M定義為



M是閉集且有關係式

關於芒德布羅集,仍有一些重要的問題未能解決。例如,芒德布羅集是否為局部連通?是否M的每一個分支都是雙曲的(即是否每個分支中存在參數w,使得Pw(z)有吸性周期點)?
芒德布羅集是最驚人的數學對象之一。圖1給出了一個芒德布羅集的圖形。仔細觀察會發現,每一處邊緣都具有“葉子”的特徵。留意圖1的底部。將其放大,得到圖2。現在,新的“葉子”成分出現了。再將圖2的底部放大,可觀察到圖3所示的令人眼花繚亂的結構。圖4和圖5是放大更多的圖形。每副圖都顯示出了一種豐富的、精細的結構。
網際網路上有很多電腦程式可用來探索芒德布羅集。(隨著圖形的放大)越來越精細的結構不斷出現。它吸引了數學、物理學和生物學上的頂尖頭腦。此外,正如下文所解釋的,這種模式是“普遍存在的”。它出現在很多看似無關的系統中。洗牌法和吉爾布雷思原理可用來描述該序列的點的排序方法。
平方與加法
從一個簡單的程式開始:平方與加法。這實際上就是定義芒德布羅集所需要的程式開始:平方與加法。這實際上就是定義芒德布羅集所需要的一切。
重複平方是人們很熟悉的一個程式。從2開始,我們會依次得到2,4,16,256,65 536,…,直到無窮。從小於1的一個數開始,如1/2,我們會依次得到1/2,1/4,1/16,1/256,1/65 536,…,該數列趨向於0。我們還要處理負數的情形。從一1開始,重複平方,會依次得到一1,1,1,1,1,1,…。如果每一次平方後再加上一個固定的數,事情就會變得更有意思了。假定每次加上1。從0開始,平方後加上1,即02+1=1,重複平方後加上1的過程,依次得12+1=2,22+1=5,52+1=26,…,直到無窮。若每次加上-1,則依次得到0,02-1=-1,(-1)2-1=0,02-1=-1,(-1)2-1=0,…。該數列永遠在0和-1之間擺動。若每次加上-2,結果也是類似的,所得數列為0,-2,2,2,2,2,…。加上一個小於-2或者大於0的數,結果都會得到一個趨於無窮的數列。加上一個-2與0之間的數,結果都會得到一個有界數列(隨著時間的推移,它們不會離0任意遠)。它們都在芒德布羅集裡。
平方與加法程式在二維上具有完美的意義,即將點z 變成點 。有一個簡單的幾何意義:二維中的點z 可通過其坐標(x,y)來刻畫。圖,6給出坐標為(x,y)的一個點以及該點與原點之間的連線,該連線與x軸的夾角為
。有一個簡單的幾何意義:二維中的點z 可通過其坐標(x,y)來刻畫。圖,6給出坐標為(x,y)的一個點以及該點與原點之間的連線,該連線與x軸的夾角為 。要得到點(x,y)的平方,可取點(x,y)到原點距離的平方以及夾角的2倍,作出新的點,其坐標為
。要得到點(x,y)的平方,可取點(x,y)到原點距離的平方以及夾角的2倍,作出新的點,其坐標為 。將其記為
。將其記為 。加上
。加上 得
得 。每次使用同一個c值,重複上述程式。從0 開始,若由該程式產生的點位於圓心在原點的足夠大的圓內,則將c歸人芒德布羅集。
。每次使用同一個c值,重複上述程式。從0 開始,若由該程式產生的點位於圓心在原點的足夠大的圓內,則將c歸人芒德布羅集。






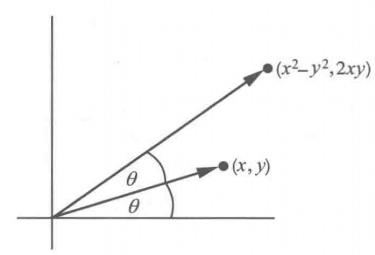 圖6
圖6周期點
加上某些特殊的數,會得到以一種固定模式循環的數列。假設每次平方後所加的數為c,則所得數列為:









採用同樣的方法,可以得到周期更大的點。例如,將 平方後加上c,得到
平方後加上c,得到 。由此得到c的兩個新的值:
。由此得到c的兩個新的值: 和
和 ,兩者都是“周期為4”的點。相應的重複數列分別是:
,兩者都是“周期為4”的點。相應的重複數列分別是:






完整的芒德布羅集
上面所有的活動都局限於一維的直線。而芒德布羅集屬於二維。二維上有一個“平方後加上c”的概念,能使重複平方後加上c所得結果有界的c,恰為芒德布羅集上的點。在平面上,c的值是二維的: 。
。

圖2給出了芒德布羅集的圖形。x軸上介於-2和0之間的值就是上面討論過的點。中央大心形區域稱為心形曲線。它的四周被斑點所包圍,而每一個這樣的斑點又被更小的斑點所包圍(以此類推,直至無窮)。關於芒德布羅集,一個主要的有待研究的問題與c的值有關(現為 ),通過“平方與加法”程式,這些值產生了周期數列。人們猜想,每一個斑點(大斑點,小斑點,以至無窮)都包含一個周期點。這個猜想如果得到了證明,那么,著名的“局部連通性”猜想也就迎刃而解了。
),通過“平方與加法”程式,這些值產生了周期數列。人們猜想,每一個斑點(大斑點,小斑點,以至無窮)都包含一個周期點。這個猜想如果得到了證明,那么,著名的“局部連通性”猜想也就迎刃而解了。

最後,讓我們解釋一下,芒德布羅集在什麼意義下是普遍存在的。對於固定的c,平方與加法程式將x變為 。當c變化時,我們得到一族不同的疊代方案。麥克馬倫(Curt McMullen)證明,平面上任何一族映射到本身的函式具有芒德布羅集的所有複雜性,包括開口、分形維度和無窮精細性。當然,這也意味著它包含了所有上面所說的吉爾布雷思排列。
。當c變化時,我們得到一族不同的疊代方案。麥克馬倫(Curt McMullen)證明,平面上任何一族映射到本身的函式具有芒德布羅集的所有複雜性,包括開口、分形維度和無窮精細性。當然,這也意味著它包含了所有上面所說的吉爾布雷思排列。

芒德布羅集和茹利亞集
分形包括多種處理過程。下面介紹兩種與眾不同的處理過程。它們能生成具有動態系統特徵的圖像。動態系統中許多有趣的問題能夠通過計算機圖形學進行探索。
假設一系列二次複變函數 定義為
定義為 。我們感興趣的是這個序列隨著n值的增加收斂還是發散。有一種直接的檢驗方法:隨著k值的增加,如果
。我們感興趣的是這個序列隨著n值的增加收斂還是發散。有一種直接的檢驗方法:隨著k值的增加,如果 有界,則函式集收斂,否則發散。注意,複數由一對實數
有界,則函式集收斂,否則發散。注意,複數由一對實數 定義,通常記為
定義,通常記為 ,這裡
,這裡 。所以有以下關係式:
。所以有以下關係式:







如果將不同的複數c套用於函式序列 ,且總是從初始值z=0開始,就能研究參數空間{c}的行為。芒德布羅(Mandelbrot)集是一個能讓具有這個初始值的函式序列收斂的複數c的集合。如果對於任何k值,
,且總是從初始值z=0開始,就能研究參數空間{c}的行為。芒德布羅(Mandelbrot)集是一個能讓具有這個初始值的函式序列收斂的複數c的集合。如果對於任何k值, ,那么序列將會發散。所以,只需簡單地檢查對於k的取值直到一個相當大的數如500時,
,那么序列將會發散。所以,只需簡單地檢查對於k的取值直到一個相當大的數如500時, 是否小於2。如果在終止序列之前,發現某個k值使
是否小於2。如果在終止序列之前,發現某個k值使 ,那么對於該複數c,就返回這樣的第一個k值;如果沒有,那么就返回0。芒德布羅集就是由返回0的複數c組成的集合。
,那么對於該複數c,就返回這樣的第一個k值;如果沒有,那么就返回0。芒德布羅集就是由返回0的複數c組成的集合。




為了用圖顯示這種情況,用2D點(a,b)來表示一個複數 ,根據之前為該複數記錄的值,用一個整數漸變色來塗染這個點。也可以採用其他的方法進行標識:每個點定義一個複數,然後運用上面提到的方法來處理這個複數,從而決定點的顏色。這樣可以得到一個2D區域,並在該區域上創建一個我們在示例代碼中描述的視窗尺寸匹配的格線,運用上面提到的方法處理每一個格線點,然後像之前那樣塗染對應的像素。圖7顯示了一幅芒德布羅集的圖像,而右邊的細節圖像則顯示了在一個更小區域內收斂的過程。圖中的整個芒德布羅集對應一個a的取值在
,根據之前為該複數記錄的值,用一個整數漸變色來塗染這個點。也可以採用其他的方法進行標識:每個點定義一個複數,然後運用上面提到的方法來處理這個複數,從而決定點的顏色。這樣可以得到一個2D區域,並在該區域上創建一個我們在示例代碼中描述的視窗尺寸匹配的格線,運用上面提到的方法處理每一個格線點,然後像之前那樣塗染對應的像素。圖7顯示了一幅芒德布羅集的圖像,而右邊的細節圖像則顯示了在一個更小區域內收斂的過程。圖中的整個芒德布羅集對應一個a的取值在 ,b在
,b在 的複數
的複數 集,而細節區域的取值為
集,而細節區域的取值為 。
。





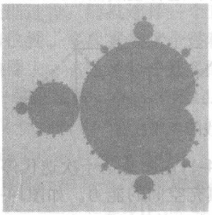 圖7(a)完整的芒德布羅集圖
圖7(a)完整的芒德布羅集圖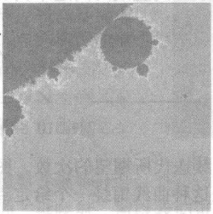 圖7(b)芒德布羅集圖細節圖
圖7(b)芒德布羅集圖細節圖對於這一系列函式 ,如果改變取固定值和變數的規則,即選擇一個固定值c,對於不同的z值計算序列函式,使用和之前相同的著色技術,那么我們可能都會問一個非常相似的問題,即這個序列是否隨著n值的增加而收斂或者發散。使得這個序列收斂的複數z的集合稱為茹利亞(Julia)集。茹利亞集與芒德布羅集有關,如果用芒德布羅集裡的任何一個複數c來生成茹利亞集時,茹利亞集將會連線起來。而如果用芒德布羅集外的一個複數c來生成茹利亞集時,茹利亞集將是完全斷開的。用芒德布羅集中非常接近邊緣的複數能夠生成非常有趣和與眾不同的茹利亞集。圖8顯示由固定點(-0.74543,11301)計算得到的特殊茹利亞集。當然也可以像顯示芒德布羅集那樣選擇其中的一小部分進行顯示,給出更為詳細和迷人的圖像。
,如果改變取固定值和變數的規則,即選擇一個固定值c,對於不同的z值計算序列函式,使用和之前相同的著色技術,那么我們可能都會問一個非常相似的問題,即這個序列是否隨著n值的增加而收斂或者發散。使得這個序列收斂的複數z的集合稱為茹利亞(Julia)集。茹利亞集與芒德布羅集有關,如果用芒德布羅集裡的任何一個複數c來生成茹利亞集時,茹利亞集將會連線起來。而如果用芒德布羅集外的一個複數c來生成茹利亞集時,茹利亞集將是完全斷開的。用芒德布羅集中非常接近邊緣的複數能夠生成非常有趣和與眾不同的茹利亞集。圖8顯示由固定點(-0.74543,11301)計算得到的特殊茹利亞集。當然也可以像顯示芒德布羅集那樣選擇其中的一小部分進行顯示,給出更為詳細和迷人的圖像。

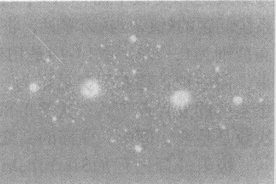 圖8
圖8
