基本介紹
- 中文名:疊代函式系統
- 外文名:Iterated Function System
- 簡稱:IFS
- 產生:具有無窮細節、精緻紋理的圖形
- 提出者:Hutchison
- 領域:計算機圖形領域
簡介


















拼貼定理













繪製分形圖形












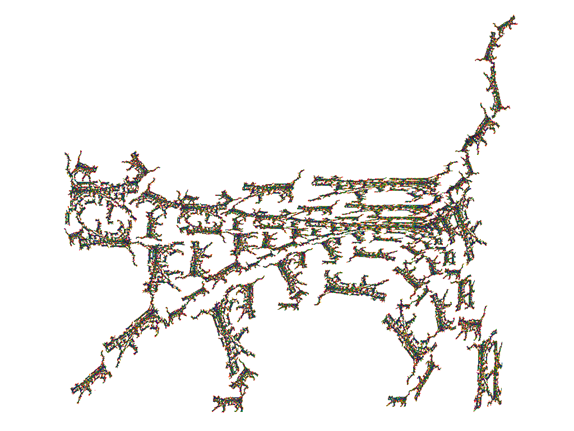











































疊代函式系統(Iterated Function System,IFS)是分形理論的重要分支。它以仿射變換為框架,根據幾何對象的整體與局部具有自相似的結構,將總體形狀以一定的機率按不同的仿射變換疊代下去,直至得到滿意的分...
在數學中,疊代函式是在碎形和動力系統中深入研究的對象。疊代函式是重複的與自身複合的函式,這個過程叫做疊代。在數學中,疊代函式是在碎形和動力系統中深入研究的對象。疊代函式是重複的與自身複合的函式,這個過程叫做疊代。介紹 通過...
將一個函式自身複合多次,便是函式的疊代。函式疊代的定義如下:設f:D→D是一個函式,對任意x∈D,記f(x)=x,f(x)=f(x),...,f(x)=f(f(x)),稱f(x)是函式f(x)在D上的n次疊代。事實上,如果疊代函式有反函式,...
《非一致壓縮疊代函式系統及其相關問題》是依託華南師範大學,由葉遠靈擔任項目負責人的面上項目。項目摘要 有限度的馬可夫動力系統(見定義1.1)可以看成是疊代函式系統的一種特殊情形。過去人們對壓縮疊代函式系統有著較深刻和廣泛的研究。
《基於MEMS光交叉的二維負反饋疊代函式系統的全光實現》是依託重慶大學,由田逢春擔任項目負責人的面上項目。中文摘要 本項目探索全光實現(二維)圖像疊代函式系統及二維負反饋的規律。信息光學系統和光計算具有高速、並行的優點,滿足高速...
L-system是一系列不同形式的正規語法規則,多被用於植物生長過程建模,但是也被用於模擬各種生物體的形態。L-system也能用於生成自相似的分形,例如疊代函式系統。起源 作為一位生物學家,Lindenmayer工作的內容是酵母菌和絲狀真菌,並研究...
函式 在數學中,疊代函式是在分形和動力系統中深入研究的對象。疊代函式是重複的與自身複合的函式,這個過程叫做疊代。模型 疊代模型是RUP(Rational Unified Process,統一軟體開發過程,統一軟體過程)推薦的周期模型。算法 疊代算法是用...
《運算元疊代與自相似集》不僅介紹運算元疊代生成的疊代函式系統和自相似集的Hausdorff測度一般理論,而且還論述了近年來關於疊代函式系統和自相似集的Hausdorff測度的若干新理論與新方法,以及相關的公開問題。《運算元疊代與自相似集》可供大學教師...
復變動態系統(Complex dynamics)是以複數空間下疊代函式定義的動態系統,以及其相關的研究。復變解析動態系統(Complex analytic dynamics)則是研究特定解析函式組成的動態系統。技巧 復變動態系統會用到以下的技巧:一般 蒙特爾定理 龐加...
《疊代函式方程的若干論題》是依託哈爾濱工業大學,由宋威擔任項目負責人的青年科學基金項目。項目摘要 疊代根問題和疊代函式方程問題是疊代理論中的重要研究對象. 疊代根問題也是動力系統的基本問題之一. 近年來, 關於疊代根的逼近和數值...
《復解函式系的隨機疊代動力系統》是依託上海大學,由周維民擔任項目負責人的青年科學基金項目。 中文摘要 經典復解析動力系統的研究局限於並單個解析函式的自身疊代,而經典疊代函式系統的研究局限於線性壓縮映照學。而本項目研究了由有限多個...
從以上步驟可以發現疊代計算搭配循環引用可以成功實現對同一個單元格反覆累加。公式中嵌套的IF函式也能正常工作,當刪除A2的值時不會錯誤地累加一次。自動添加不更新的時間 Excel有一個時間函式Now,它可以生成當前系統時間。函式運算結果在...
複合離散混沌系統是一類特殊的混沌系統,它由兩個(或多個)離散混沌系統通過一定的規則構成與離散混沌系統相比,複合離散混沌系統的疊代過程不僅具有對初始條件的敏感性,而且具有依照雙序列選擇疊代函式的靈活性,因此疊代過程還具有一定的隨機性...
2.6尋找Rd上可微函式f(x)的最小值位置的模擬退火算法224 2.7Dobrushin 不等式、指數遍歷性與收斂性225 3隨機的疊代函式系統228 3.1局部相似性的基本想法228 3.2輪廓圖全體組成的距離空間229 3.3灰度圖與隨機疊代函式系統233 4...
