基本介紹
- 中文名:疊代函式
- 外文名:Iterative function
介紹
當軌道的點會聚於一個或多個極限的時候,軌道的會聚點的集合叫做極限集合或ω-極限集合。
吸引和排斥的想法類似推廣;依據在疊代下小鄰域行為,可把疊代分類為穩定集合和不穩定集合。
其他極限行為也有可能;比如,遊蕩點是總是移動永不回到甚至接近起點的點。
定義
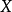
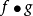

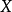
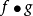

疊代算法是用計算機解決問題的一種基本方法。它利用計算機運算速度快、適合做重複性操作的特點,讓計算機對一組指令(或一定步驟)進行重複執行,在每次執行這組指令(或...
函式疊代法(function iteration method)亦稱函式空間疊代。動態規劃的求解方法之一是以段數作為參變數,先求在各個不同段數下的最優策略,然後從對應的最優解中選...
疊代函式系統(Iterated Function System,IFS)是分形理論的重要分支 。它以仿射變換為框架,根據幾何對象的整體與局部具有自相似的結構,將總體形狀以一定的機率按不同...
疊代是重複反饋過程的活動,其目的通常是為了逼近所需目標或結果。每一次對過程的重複稱為一次“疊代”,而每一次疊代得到的結果會作為下一次疊代的初始值。重複執行...
疊代法是數值計算中一類典型方法,套用於方程求根,方程組求解,矩陣求特徵值等方面。其基本思想是逐次逼近,先取一個粗糙的近似值,然後用同一個遞推公式,反覆校正此...
疊代法也稱輾轉法,是一種不斷用變數的舊值遞推新值的過程,跟疊代法相對應的是直接法(或者稱為一次解法),即一次性解決問題。疊代算法是用計算機解決問題的一種...
《函式疊代與函式方程》是2010年上海科技教育出版社出版的圖書,作者是王偉葉、熊斌。本書主要是對函式疊代和函式方程的進行介紹和說明。...
疊代結構(iteration structure)亦稱循環結構,是最重要的控制結構,也是軟體設計人員需要掌握的基本技能。當條件成立的時候,執行循環體的代碼,當條件不成立的時候,跳出...
用於快速選擇的非遞歸實現算法——循環疊代算法,與遞歸算法以及V c++標準庫函式nth_element進行了比較,表明該算法比傳統的遞歸算法具有較高的效率和可靠性; 與標準...
牛頓疊代法(Newton's method)又稱為牛頓-拉夫遜(拉弗森)方法(Newton-Raphson method),它是牛頓在17世紀提出的一種在實數域和複數域上近似求解方程的方法。...
疊代器(iterator)有時又稱游標(cursor)是程式設計的軟體設計模式,可在容器(container,例如鍊表或陣列)上遍訪的接口,設計人員無需關心容器的內容。...
在計算機科學中,疊代深化搜尋(iterative deepening search)或者更確切地說疊代深化深度優先搜尋 (iterative deepening depth-first search (IDS or IDDFS)) 是一個...
平方根疊代法(square root iterative method一種具有大範圍收斂性的方程求根疊代法.設.f<x是階數小於2的整函式,若f(二)只含實零點,則求方程.f<二)=0根的...
函式方程是含有未知函式的方程。函式方程可以有一個解,可以無解,也可以有多個解,甚至可以有無窮多個解。能使函式方程成立的函式叫做函式方程的解,求函式方程的解...
斜坡函式是一元實函式,因其圖像像斜坡而得名。斜坡函式在負半軸函式值為零,正半軸為形如y=At的正比例函式。A=1時,稱為單位斜坡函式。斜坡函式是系統動力學...
疊代,特別是復變函式的疊代,介紹動力系統中渾沌現象的產生及其數學含義,介紹復疊代中所產生的複雜幾何圖形??分形,並介紹受到廣泛關注的Mandelbrot集合。...
函式XIRR 與淨現值函式 XNPV 密切相關。 函式 XIRR 計算的收益率即為函式 XNPV = 0 時的利率。Excel 使用疊代法計算函式 XIRR。 通過改變收益率(從 guess 開始...
阿克曼函式(Ackermann)是非原始遞歸函式的例子。它需要兩個自然數作為輸入值,輸出一個自然數。它的輸出值增長速度非常快,僅是對於(4,3)的輸出已大得不能準確計算...
RATE函式基於等額分期付款的方式,返回某項投資或貸款的實際利率。RATE函式通過疊代法計算得出結果,並且可能無解或有多個解。如果在進行20次疊代計算後,RATE函式的...
標準函式,是具有常用功能的函式。在程式設計中,常將一些常用的功能模組編寫成的函式放在函式庫中供公共選用,一般稱為標準函式。程式是由若干個程式模組組成的,高級...
